java基础、数据结构、安卓相关基础
- 1.数组
- 2.有序数组
- 3.栈
- 4.队列
- 5.二叉树
- 6.红黑树
- 7.哈希表
- 8.堆
- 10.图
- 常见的算法
- Vector和Stack的细节
- LinkedList的细节
- SynchronizedList的细节
- gc优化
- Android的DVM和ART
- 什么是运行时?
- 1.汇编器
- 2.编译器
- 3.解释器
- JAVA 代码是怎么执行的?
- Android 代码是怎么执行的
- Just In Time (JIT)
- Ahead Of Time(AOT)
- Android 为什么要使用虚拟机?
- ART 的优点
- ART 的缺点
- 结论
- Activity
- Handler
- HandlerThread
- AsyncTask
- Binder
- View事件传递
- View的绘制流程
- SurfaceView的使用
- IntentService替换Service的场景
- Service保活
- Android序列化方式和区别
- NDK和JNI
- 插件化和热修复
- RxJava
- Glide
- OKHttp
- MVC、MVP和MVVM
- Gradle和Groovy
- TCP/HTTP
- SQL
- 自动化测试
- 抓包
1.数组
数组的特性就不做介绍了。
2.有序数组
有序数组自然指的是排过序的数组
3.栈
栈的特性,后进先出。通过利用栈的特性可以完成一些特殊功能需求的设计,比如:android中的任务栈。
在java中栈的基本操作如下:
java中栈(stack)的基本使用方式:
//初始化
Stack stack=new Stack
//判断是否为空
stack.empty()
//取栈顶值(不出栈)
stack.peek()
//进栈
stack.push(Object);
//出栈
stack.pop();
通过stack的定义,我们可以知道两点:
a.stack的功能实现是依赖于数组的,所以stack最终存储数据的数据结构是数组;
b.stack中所有的操作方法都是同步的,所以stack是线程安全的。
一下是java中stack的基本定义:
public class Stack<E> extends Vector<E> {
public Stack() {
}
public E push(E item) {
addElement(item);
return item;
}
public synchronized E pop() {
E obj;
int len = size();
obj = peek();
removeElementAt(len - 1);
return obj;
}
public synchronized E peek() {
int len = size();
if (len == 0)
throw new EmptyStackException();
return elementAt(len - 1);
}
public boolean empty() {
return size() == 0;
}
public synchronized int search(Object o) {
int i = lastIndexOf(o);
if (i >= 0) {
return size() - i;
}
return -1;
}
private static final long serialVersionUID = 1224463164541339165L;
}
可以看到Stack的基础功能由其父类Vector实现,在父类Vector中通过Object[]来存储相应的数据内容。我们可以开一下Vector中removeElementAt()的实现:
public synchronized void removeElementAt(int index) {
modCount++;
if (index >= elementCount) {
throw new ArrayIndexOutOfBoundsException(index + " >= " +
elementCount);
}
else if (index < 0) {
throw new ArrayIndexOutOfBoundsException(index);
}
int j = elementCount - index - 1;
if (j > 0) {
System.arraycopy(elementData, index + 1, elementData, index, j);
}
elementCount--;
elementData[elementCount] = null; /* to let gc do its work */
}
4.队列
队列的基本特性是先进先出,我们在讲到android中handler-looper的消息队列处理时会经常提到消息队列这个概念,这里的消息队列就是一种队列数据结构。
在java的util库定义了基本的队列数据结构Queue:
public interface Queue<E> extends Collection<E> {
boolean add(E e); //向队列中添加element
boolean offer(E e); //相对列中添加element,这个方法在LinkedList中的实现是调用add方法。从Queue的注释中可以发现,这个方法在处理一些有长度限制的队列时可保证在长度超过队列长度限制时返回false而不是抛出异常。
E remove(); //移除队列前端的element,并返回element
E poll(); //功能同上,这个方法在集合为空时会犯返回null而不是抛出异常。
E element(); //获取队列的第一个element
E peek(); //功能同上,这个方法在集合为空时不会抛出异常,并返回null
}
Queue只是一个接口,它有很多实现方式,包括多个继承自它的接口,比如:AbstractQueue、BlockingQueue、Deque、ConcurrentLinkedQueue等。
举个例子:LinkedList就实现了Deque,所以我们可以使用LinkedList来实现队列的功能。
队列有多重不同的实现方式,依据使用的场景不同、功能不同,我们需要选择不同的队列来实现功能。
常见的队列结构通常继承自一下几个接口:Queue、BlockingQueue、Deque(双端队列)
5.二叉树
6.红黑树
红黑树是一种自平衡的二叉树,也就是2-3-4树的一种。红黑数在我们常用的数据结构类型HashMao中有实际的应用。
理解红黑树需要先了解两个知识点:二叉查找树和完美平衡二叉树。
首先,什么是二叉查找树?
二叉查找树又称二叉排序树,二叉排序树满足一下几个特征:
1.首先它是一个二叉树满足二叉树的定义,或者是一颗空树;
2.若左子树不为空,那么左子树上所有的节点的值均小于根节点;
3.若友字数不为空,那么右字数上的所有节点的值均大于根节点;
4.没有键值相等的节点。
什么是完美平衡二叉树呢?
首先,平衡二叉树指的是一颗空树或者它的左子树和右子树的高度差不大于1,并且左右子树都是一颗平衡二叉 树。在平衡二叉树的基础上,完美平衡二叉树就是一个深度为k且有2^(k+1)个节点的二叉树。换句话说,这是一 个满二叉树,在这个二叉树上,要么就是没有子节点的叶子节点,要么就是有两个叶子节点的根节点,并且每 一层都占满,没有空位。
了解了以上两个概念,我们再往下学习红黑树的概念。首先,红黑树也是二叉查找树并且是一个平衡二叉树(平衡二叉排序树),从概念上讲,红黑树是二叉查找树的一种。所以红黑树满足所有二叉查找树的定义(定义如上已给出)。那么红黑树在二叉查找树的定义上又规定了哪些特性呢?
- 性质1:每个节点要么是黑色,要么是红色;
- 性质2:根节点是黑色的;
- 性质3:每个叶子节点(NIL)是黑色的;
- 性质4:每个红色节点的两个子节点一定都是黑色的;
- 性质5:任意一节点到每个叶子节点的路径都包含数量相同的黑节点。
这5条性质网上每个讲红黑树的帖子都能看到,但是这5条性质却不是每个人都能一眼看懂的。有个坑,首先,我们不讨论什么是黑色节点什么是红色节点。上述性质3中提到的叶子节点称之为NIL节点,转换到java中其实指的就是NULL节点,所以红黑树性质中的叶子节点指的并不是我们平常概念意义上的叶子节点,而是叶子节点下两个为null的引用。理解了这个NIL节点的定义后我们再看第5条性质就很好理解了,我们参照下面这张图(图片来自简书-安卓大叔的帖子)
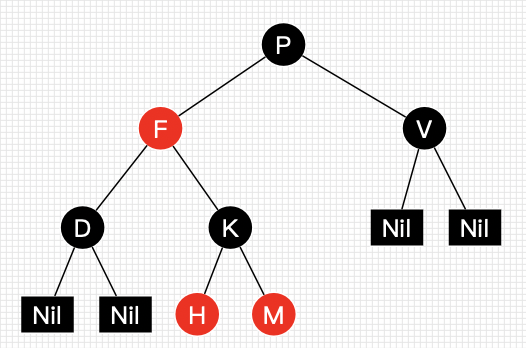
图中的Nil节点其实都是空节点,图上任意一个节点到叶子节点的简单路径都有相同的黑节点数目,并且我们可以得出一个推论,如果一个节点存在黑子节点,那么它一定有另一个黑子节点。另附一张更清晰的概念图(图像来自CSDN):
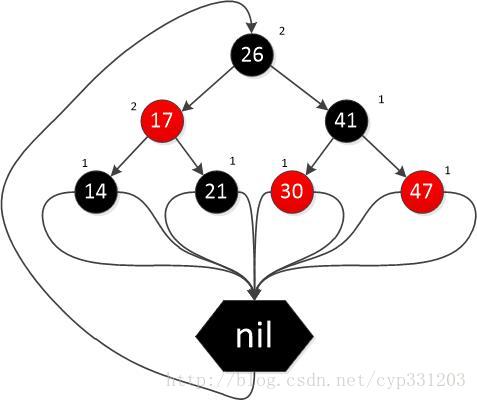
图上标注的是所有节点到他的叶子节点所包含的黑色节点数量。所有的叶子节点都是nil。
关于红黑树插入变换的两个旋转操作的解释:
左旋:以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。
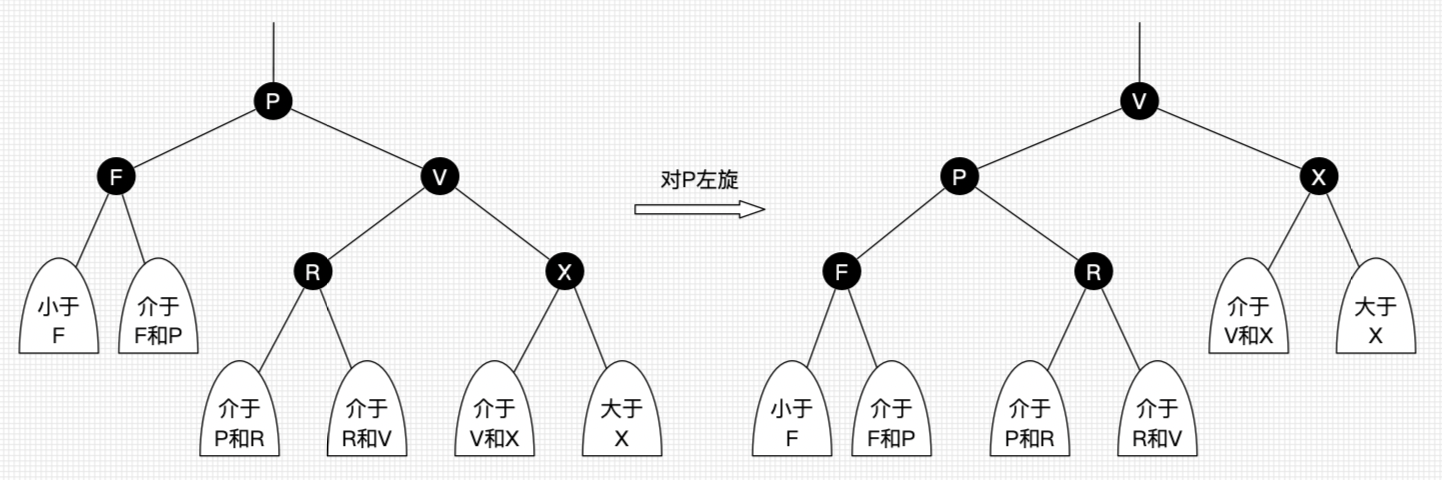
右旋:以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变。
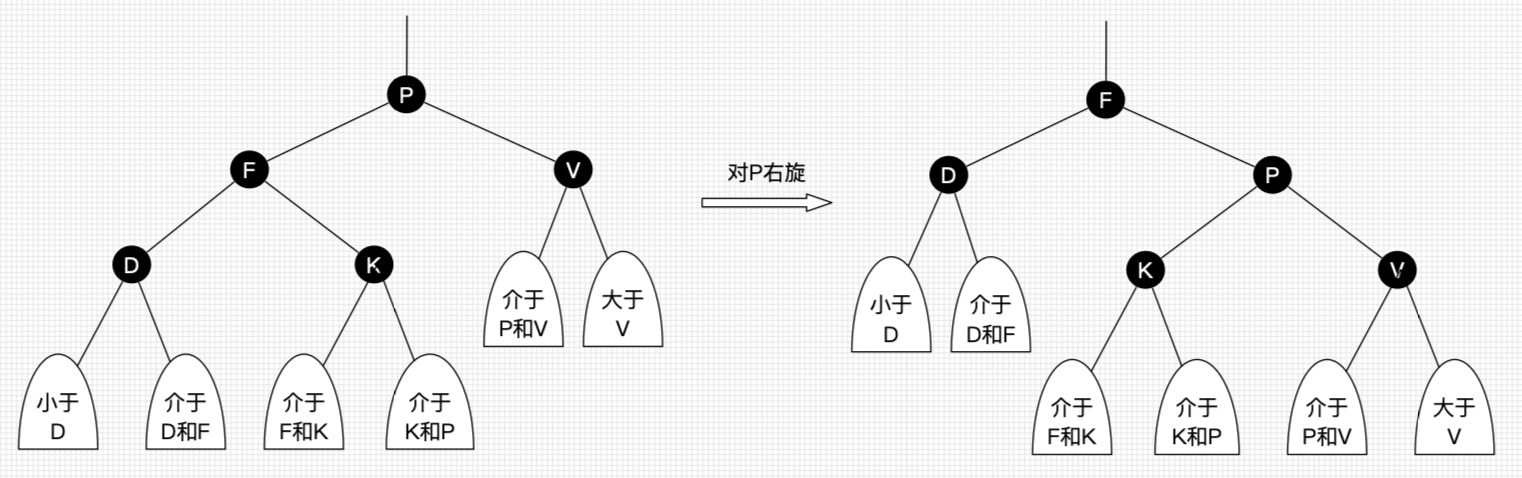
通过以上图片展示可以观察到:
左旋只影响旋转结点和其右子树的结构,把右子树的结点往左子树挪了。 右旋只影响旋转结点和其左子树的结构,把左子树的结点往右子树挪了。
以上是红黑树除了节点颜色之外的所有概念及定义。接下来看一下,到底什么是黑节点,什么是红节点,他们到底有什么用,以及最关键的,我们要搞明白什么时候这个节点是红色的,什么时候是黑色的。
二叉树的基本作用是数据的插入和查找,尤其是查找,我们设计二叉树的初衷就是为了方便查找,方便检索数据。那么红黑树的查找过程就很简单,因为它是一个二叉排序树,查找的过程无非是一下几步:
-
从根结点开始查找,把根结点设置为当前结点;
-
若当前结点为空,返回null;
-
若当前结点不为空,用当前结点的key跟查找key作比较;
-
若当前结点key等于查找key,那么该key就是查找目标,返回当前结点;
-
若当前结点key大于查找key,把当前结点的左子结点设置为当前结点,重复步骤2;
-
若当前结点key小于查找key,把当前结点的右子结点设置为当前结点,重复步骤2;
我们知道,二叉排序树是保证所有节点的左子树节点都小于根节点,所有右子树的节点都大于根节点,所以二叉排序树的查找效率比较高O(2lgN),但是在一些特殊的二叉排序树中,其查找效率并不会比一般的链表要高,比如单支树O(N)。所以当我们在查找的这个树是一颗平衡二叉排序树时我们才可以保证这颗树的最差查找效率也能够达到O(2lgN)。所以平衡二叉排序树的插入算法就很重要,为了得到较高的查找效率,我们不得不设计一些有效的插入算法来保证我的二叉排序树它始终是平衡的。红黑树的名称就来源自它的插入算法。
红黑树到底是如何插入节点的呢?
红黑树的节点插入过程一般分为三步:查找、插入、调整平衡;
查找的过程比较简单和上面的二叉排序树的查找过程相似,查找的最终目的是找到当前插入节点的插入位置,具体过程如下:
从根结点开始查找;
若根结点为空,那么插入结点作为根结点,结束。
若根结点不为空,那么把根结点作为当前结点;
若当前结点为null,返回当前结点的父结点,结束。
若当前结点key等于查找key,那么该key所在结点就是插入结点,更新结点的值,结束。
若当前结点key大于查找key,把当前结点的左子结点设置为当前结点,重复步骤4;
若当前结点key小于查找key,把当前结点的右子结点设置为当前结点,重复步骤4;
找到相应的插入位置以后就可以将节点插入到红黑树中,那么当前插入的节点就是红色的,为什么一定是红色的呢?答案可以从红黑树的特性中找到,当插入的节点是红色时不会破坏当前子树的黑色平衡即不会破坏特性5,但是当插入的节点是黑色时一定会破坏特性5。红黑树插入新节点的情况可以归结为下图几种:

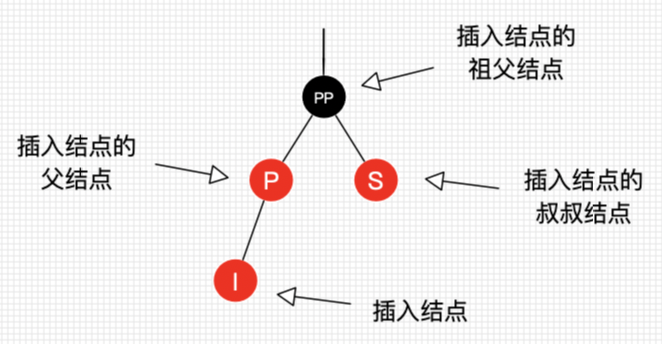
以上图列出的几种插入情形为序,我们分别来讨论下插入操作的过程。
插入情景1:红黑树为空树
这种情况最为简单,直接把插入的节点作为根节点,并设置为黑色节点(由红黑树的特性决定)
插入情景2:插入节点的key已存在
查找到节点所在位置之后,将插入节点的颜色设置为当前节点的颜色,然后将当前节点的值设置为插入节点的 值。
插入情景3:插入节点的父节点为黑色节点
当插入节点的父节点为黑色时,插入节点为红色不会影响当前子树的黑色值可以直接插入。
插入情景4:插入节点的父节点为红色节点
这种情况有一个影藏的前提,如果插入节点的父节点为红色,那么这个父节点不可能为根节点,并且这个父节 点一定还有上层节点。在这种情况下又会有几种不同的情形:
插入情形4.1:叔叔节点存在并且为红节点
处理的过程如下:
将P和S设置为黑色
将PP设置为红色
把PP设置为当前插入点


插入情景4.2:叔叔节点不存在或为黑节点,并且插入节点的父亲节点是祖父节点的左子节点。
通过之前的性质5的推论,当兄弟节点不是红色节点时则一定是叶子节点(NIL),如果兄弟节点不是叶子节 点的黑色节点则子树将不是黑色平衡,不满足性质5。在此情景下又有两种情况:
插入情景4.2.1:插入节点是其父节点的左子节点
处理方式为:
将P设置为黑色
将PP设置为红色
对PP进行右旋

插入情景4.2.2:插入节点是其父节点的右子节点
处理方式:
对P进行左旋
把P设置为插入节点,得到情景4.2.1
进行情景4.2.1的处理
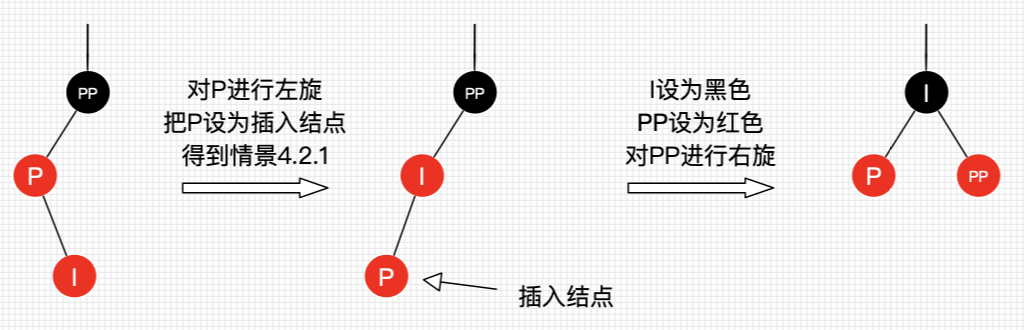
插入情景4.3:叔叔节点不存在或为黑节点,并且插入节点的父亲节点是祖父节点的右子节点
插入情景4.3.1:插入节点是其父节点的右子节点
处理过程:
将P设置为黑色
将PP设置为红色
对PP进行左旋
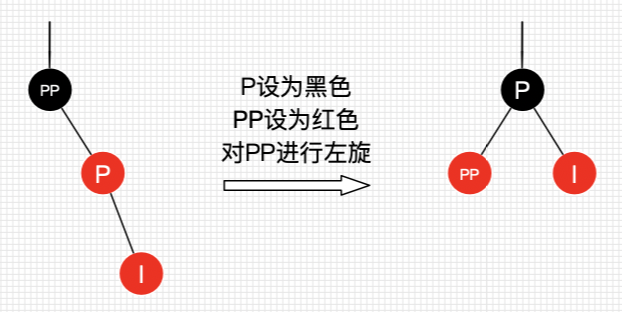
插入情景4.3.2:插入节点是其父节点的左子节点
处理过程:
对P进行右旋
把P设置为插入节点,得到情景4.3.1
进行4.3.1的处理
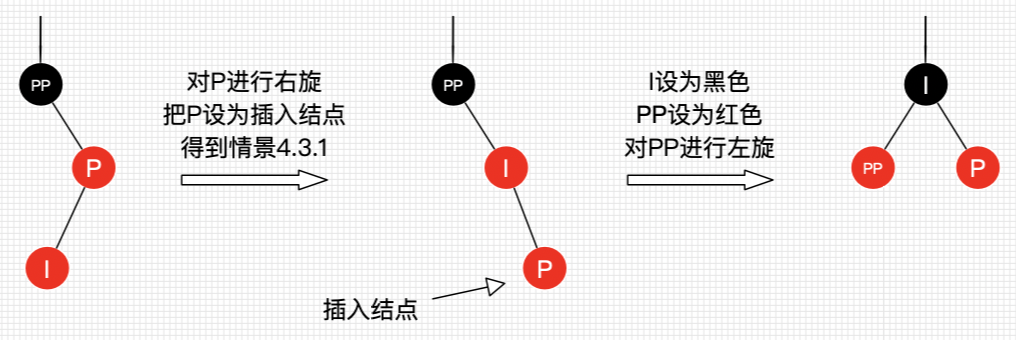
以上,所有插入情形都介绍完毕。
红黑树除了在添加节点是需要保证树的平衡性(黑高平衡),在删除节点时也需要保持平衡。在删除节点时同样需要分情况进行处理。
红黑树的删除操作也包括两个部分的工作:一查找目标节点,二删除后自平衡。查找节点的过程和之前的查找方式一致不讨论。删除后自平衡需要处理的情况可以归纳为以下几种:
其一,若删除的节点无子节点,直接删除
其二,若删除的节点只有一个子节点,用子节点替换删除节点
其三,若删除节点有两个子节点,用后继节点(大于删除节点的最小节点)替换删除节点
这里说明下什么是大于删除节点的最小节点。首先,大于删除节点的节点在删除节点的右子树上。其次,右子树上的最小节点是右子树上最左的节点。
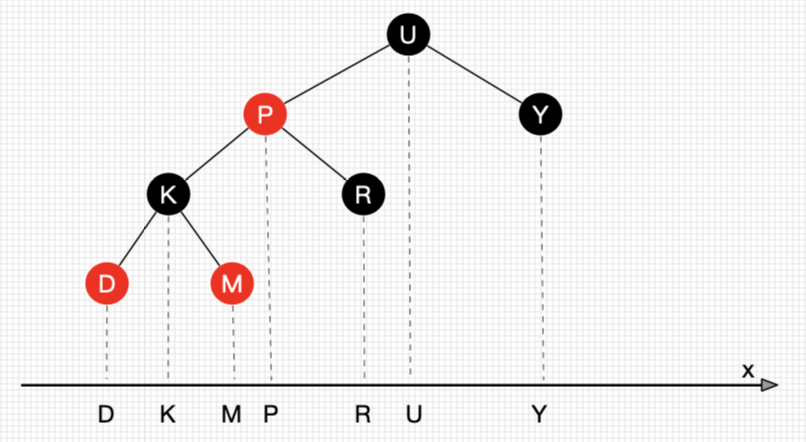
所有节点投射到X轴上都是从左往右有序的,被删除节点可以被后继节点替代,自然也能被前继节点替代。比如删除P节点,则其后继节点就是其右子树最左节点即R,前继节点就是其左子树最右节点M。
在分析红黑树的删除情况之前,有一个重要的思路可以掌握,即:删除节点被替代后,在不考虑节点的键值的情况下,对于树来说,可以认为删除的是替代节点。如图:
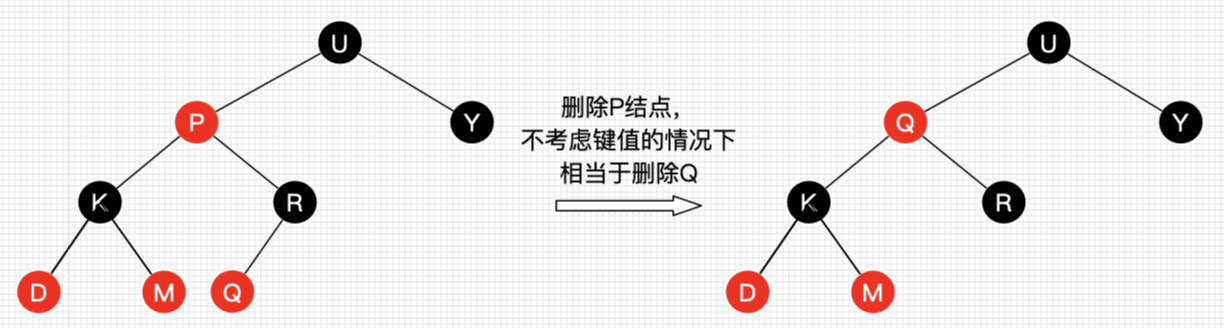
删除节点P的最终结果是删除了其替代节点Q位置上的节点(我们是不是可以认为最终的结果是将节点Q删除,然后将Q的值赋给P呢?)
下面来分别分析这三种删除的情况,
第一种情况直接删除,不作讨论。
第二种情况,删除节点用其唯一的子节点直接替换,替换后可以认为是子节点被删除,则子节点被删除又会产生以上三种删除的情况,即:子节点没有子节点则直接删除;子节点有一个子节点则直接替换;子节点有两个子节点则用后继节点替换之。这是一个递归的过程。
第三中情况其实是删除后继节点,那么后继节点也会有三种情况,即:没有子节点、一个子节点、两个子节点。
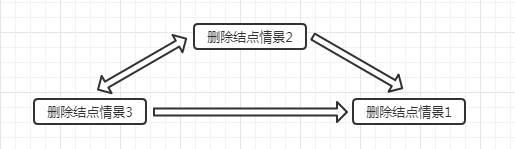
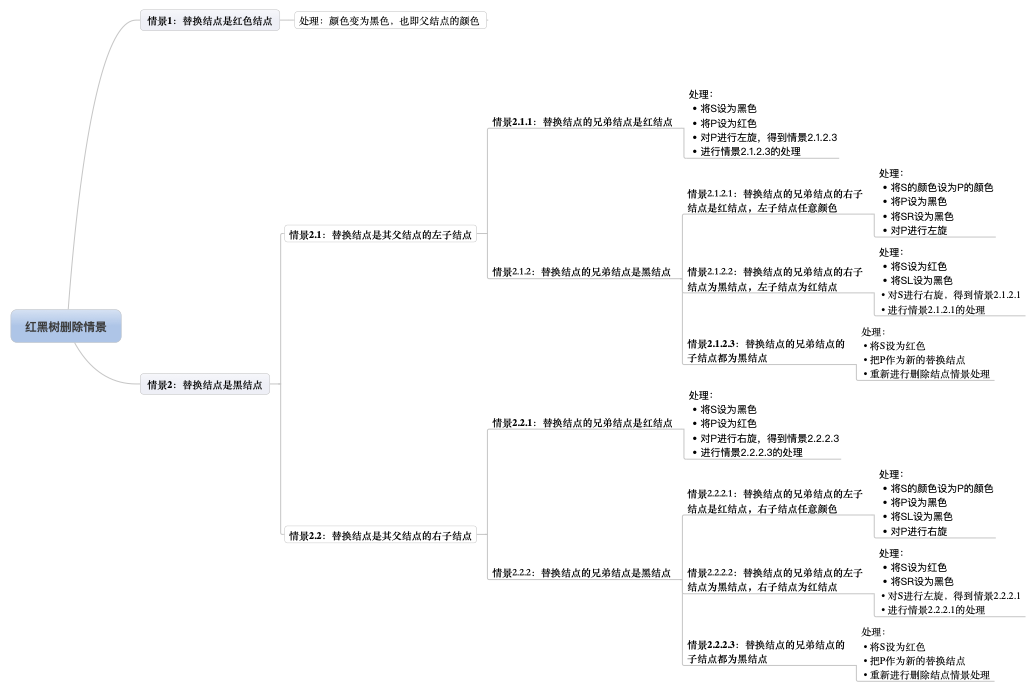
上图列出了所有删除的情况,我们在分别讨论这些删除情况之前先约定几个表示节点的概念以方便描述,如下图:
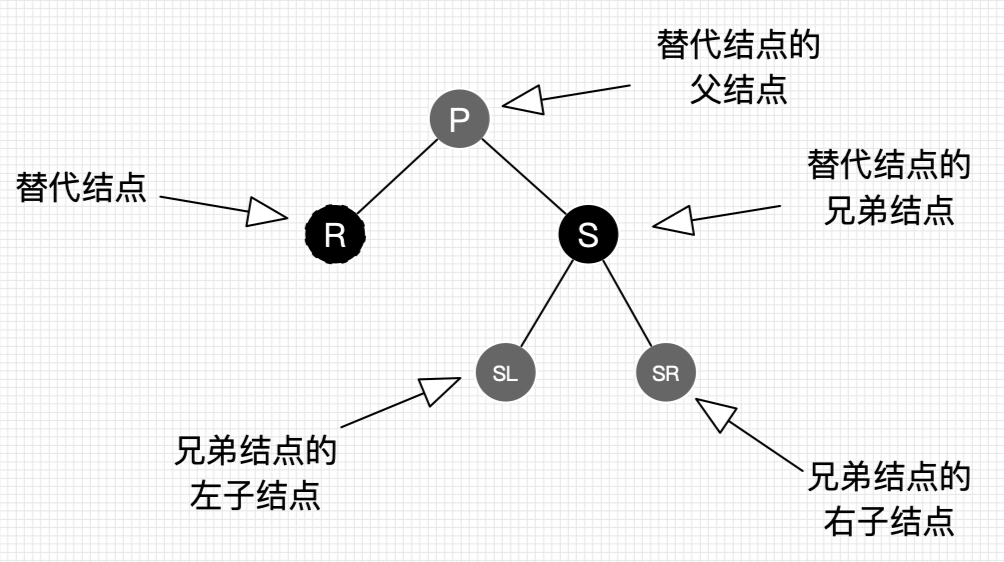
删除情景1:替换节点是红色节点
我们把替换的节点换到了删除节点的位置时,由于替换节点是红色,删除也了也不会影响红黑树的平衡,只要把替换节点的颜色设置为删除的节点的颜色即可重新平衡。
处理:颜色变为删除节点的颜色
删除情景2:替换节点是黑色
当替换节点是黑色时需要进行自平衡的处理,我们必须还得考虑替换节点是其父节点的左子节点还是右子节点,来做不同的旋转操作,使树平衡。
删除情景2.1:替换节点是其父节点的左子节点
删除节点2.1.1:替换节点的兄弟节点是红色节点
若兄弟节点是红色的,那么根据性质4,兄弟节点的父节点和子节点肯定为黑色,不会有其他情景。
处理:
将S设为黑色
将P设为红色
对P进行左旋,得到情景2.1.2.3
进行情景2.1.2.3的处理

删除情景2.1.2:替换节点的兄弟节点是黑色节点
当兄弟节点为黑色是,其父节点和子节点的具体颜色无法确定,此时需要考虑多种情况:
删除情景2.1.2.1:替换节点的兄弟节点的右子节点是红色节点,左子节点任意颜色
即将删除的左子树的一个黑色节点,显然左子树的黑色节点少了1,
处理:
将S的颜色设置为P的颜色
将P设置为黑色
将SR设置为黑色
将P进行左旋

从图上的结果我们很容易以为变换的结果没有保持黑色平衡,那是因为图上浅色的节点是没有固定颜色 的,并且这只是整个红黑树的一部分图形。
删除情景2.1.2.2:替换节点的兄弟节点的右子节点为黑色节点,左子节点为红色节点
兄弟节点所在的子树有红节点,我们总可以向兄弟子树借一个红节点过来,显然该情景可转换为情景 2.1.2.1。
处理:
将S设为红色
将SL设为黑色
对S进行右旋,得到情景2.1.2.1
进行情景2.1.2.1的处理
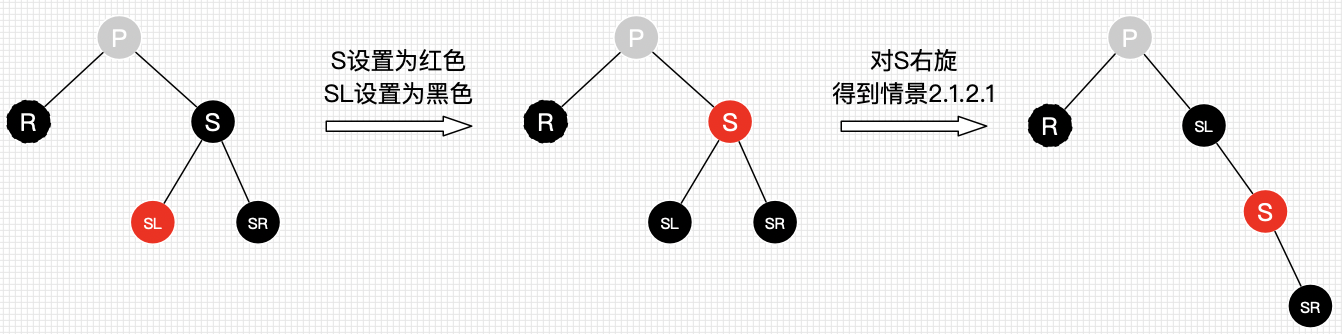
删除情景2.1.2.3:替换节点的兄弟节点的子节点都为黑色
处理:
将S设为红色
把P作为新的替换节点
重新进行删除节点情景处理

删除情景2.2:替换节点是其父节点的右子节点
删除情景2.2.1:替换节点的兄弟节点是红色节点
处理:
将S设为黑色
将P设为红色
对P进行右旋,得到情景2.2.2.3
对情景2.2.2.3进行处理

删除情景2.2.2:替换节点的兄弟节点是黑色节点
删除情景2.2.2.1:替换节点的兄弟节点是红色
处理:
将S设为黑色
将P设为红色
对P进行右旋,得到情景2.2.2.3
对情景2.2.2.3进行处理

删除情景2.2.2.2:替换节点的兄弟节点的左子节点为黑色,右子节点为红色
处理:
将S设为红色
将SR设为黑色
对S进行左旋,得到场景2.2.2.1
对情景2.2.2.1进行处理
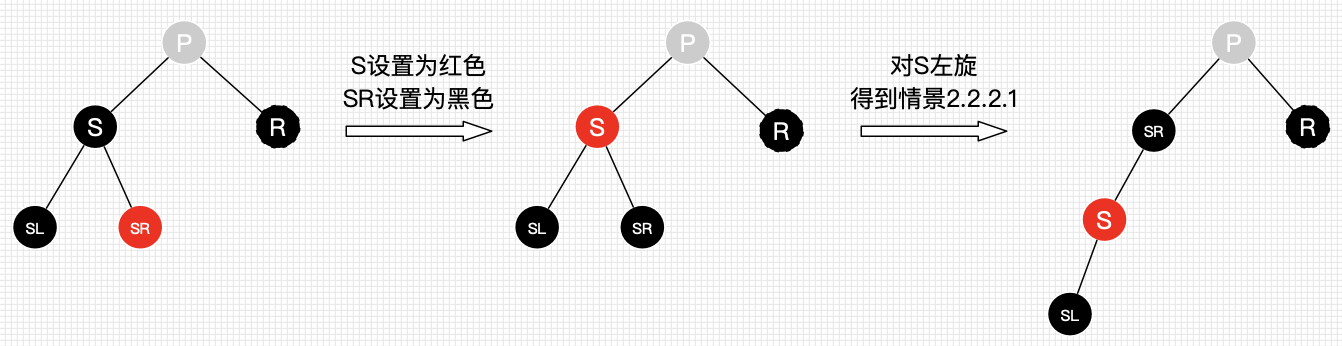
删除情景2.2.2.3:替换节点的兄弟节点的子节点都为黑色
处理:
将S设为红色
把P作为新的替换节点
重新进行删除节点情景处理
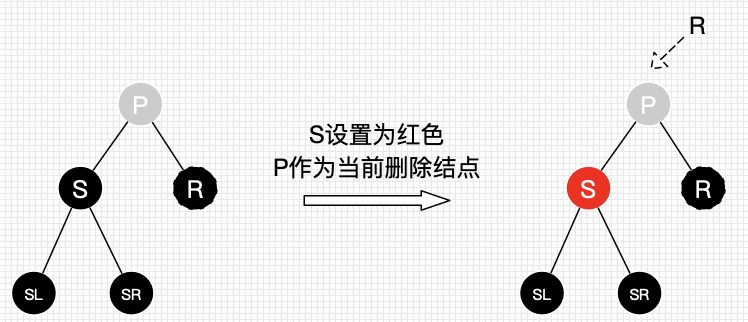
删除节点的处理分析完毕,总结删除的几个原则:
- 自己能搞定的自消化(情景1)
- 自己不能搞定的叫兄弟帮忙(除了情景1、情景2.1.2.3和情景2.2.2.3)
- 兄弟都帮忙不了的,通过父母,找远方亲戚(情景2.1.2.3和情景2.2.2.3)
一下是一个java红黑树的代码实现:
/**
* 节点定义
*/
public static class Node {
private long value;
private Node left; //左孩子
private Node right;//右孩子
private int color; //0-黑色,1-红色
private int childType; //0-left, 1-right, -1-未指定
private Node parent; //父节点
public Node(long value, Node left, Node right, int color, Node parent) {
this.value = value;
this.left = left;
this.right = right;
this.color = color;
this.parent = parent;
}
public Node(long value) {
this.value = value;
}
public Node(long value, int color){
this.value = value;
this.color = color;
}
public int getChildType() {
return childType;
}
public void setChildType(int childType) {
this.childType = childType;
}
public long getValue() {
return value;
}
public void setValue(long value) {
this.value = value;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
if (left!=null){
this.left.setChildType(0);
this.left.setParent(this);
}
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
if (right != null) {
this.right.setChildType(1);
this.right.setParent(this);
}
}
public int getColor() {
return color;
}
public void setColor(int color) {
this.color = color;
}
public Node getParent() {
return parent;
}
public void setParent(Node parent) {
this.parent = parent;
if (parent == null) {
childType = -1;
}
}
}
public static class RBTree{
private Node root;
public RBTree(Node root) {
this.root = root;
}
public Node getRoot() {
return root;
}
public void setRoot(Node root) {
this.root = root;
}
/**
* 查找插入点的父节点
* @param node
* @return
*/
private Node searchInsertParent(Node node, Node currentNode) {
if (currentNode.getValue() == node.getValue()) {
//如果已存在则替换当前节点
node.setLeft(currentNode.getLeft());
node.setRight(currentNode.getRight());
if (currentNode.getParent() != null) {
if (currentNode.getChildType() == 0) {
currentNode.getParent().setLeft(node);
} else {
currentNode.getParent().setRight(node);
}
} else {
root = node;
}
return null;
} else if (currentNode.getValue()>node.getValue()){
if (currentNode.getLeft()!=null) {
return searchInsertParent(node, currentNode.getLeft());
} else {
currentNode.setLeft(node);
return currentNode;
}
} else {
if (currentNode.getRight()!=null){
return searchInsertParent(node,currentNode.getRight());
} else {
currentNode.setRight(node);
return currentNode;
}
}
}
/**
* 查找节点
* @param value
* @return
*/
public Node searchNode(long value) {
return searchNode(value,root);
}
public Node searchNode(long value, Node currentNode) {
if (currentNode!=null){
if (currentNode.getValue() == value) {
return currentNode;
} else if (currentNode.getValue()<value) {
return searchNode(value, currentNode.getRight());
} else {
return searchNode(value, currentNode.getLeft());
}
}
return null;
}
/**
* 左旋
* @param currentNode
*/
public void leftRound(Node currentNode){
Node parentNode = currentNode.getParent();
Node rightNode = currentNode.getRight();
Node rightLeftNode = rightNode.getLeft();
if (parentNode != null) {
if (currentNode.getChildType() == 0) {
parentNode.setLeft(rightNode);
} else {
parentNode.setRight(rightNode);
}
} else {
rightNode.setParent(null);
root = rightNode;
}
rightNode.setLeft(currentNode);
currentNode.setRight(rightLeftNode);
}
/**
* 右旋
* @param currentNode
*/
public void rightRound(Node currentNode){
Node parentNode = currentNode.getParent();
Node leftNode = currentNode.getLeft();
Node leftRightNode = leftNode.getRight();
if (parentNode != null) {
if (currentNode.getChildType() == 0) {
parentNode.setLeft(leftNode);
} else {
parentNode.setRight(leftNode);
}
} else {
leftNode.setParent(null);
root = leftNode;
}
leftNode.setRight(currentNode);
currentNode.setLeft(leftRightNode);
}
/**
* 按行打印当前树
*/
public void printTree() {
ArrayList<Node> nodes = new ArrayList<>();
nodes.add(root);
ArrayList<Node> tmp = new ArrayList<>();
while (nodes.size()>0) {
for (int i = 0; i < nodes.size(); i++) {
if (nodes.get(i) == null){
System.out.print("nil ");
} else {
if (nodes.get(i).getColor() == 1) {
System.out.print("^"+nodes.get(i).getValue()+" ");
} else {
System.out.print(nodes.get(i).getValue()+" ");
}
if (nodes.get(i).getLeft()!=null) {
tmp.add(nodes.get(i).getLeft());
} else {
tmp.add(null);
}
if (nodes.get(i).getRight()!=null) {
tmp.add(nodes.get(i).getRight());
} else {
tmp.add(null);
}
}
}
System.out.println();
nodes.clear();
nodes.addAll(tmp);
tmp.clear();
}
}
/**
* 寻找当前节点的后继节点
* @param currentNode
* @return
*/
private Node findNextNode(Node currentNode) {
if (currentNode==null){
return null;
}
if (currentNode.getLeft()==null) {
return currentNode;
} else {
return findNextNode(currentNode.getLeft());
}
}
/**
* 交换节点值
* @param targetNode
* @param replaceNode
*/
private void switchValue(Node targetNode, Node replaceNode) {
long tmpValue = targetNode.getValue();
targetNode.setValue(replaceNode.getValue());
replaceNode.setValue(tmpValue);
}
/**
* 处理替代节点的黑色平衡
* @param targetNode
* @param rNode
*/
private void evalTree(Node targetNode, Node rNode){
//替换节点为红色,直接设置为删除节点的颜色
if (rNode.getColor() == 1) {
rNode.setColor(targetNode.getColor());
}
//替换节点为黑色
Node parent = rNode.getParent();
if (rNode.getColor() == 0) {
//替换结点是其父结点的左子结点
if (rNode.getChildType() == 0) {
if (parent.getRight() != null) {
//替换结点的兄弟结点是红结点
if (parent.getRight().getColor()==1) {
parent.getRight().setColor(0);
parent.setColor(1);
leftRound(parent);
parent = rNode.getParent();
parent.getRight().setColor(1);
evalTree(targetNode, parent);
return;
}
//替换节点的兄弟节点是黑色的
if (parent.getRight().getColor()==0) {
//替换节点的兄弟结点的右子结点是红结点
if (parent.getRight().getRight()!=null &&
parent.getRight().getRight().getColor()==1) {
parent.getRight().setColor(parent.getColor());
parent.setColor(0);
parent.getRight().getRight().setColor(0);
leftRound(parent);
}
//替换结点的兄弟结点的右子结点为黑结点,左子结点为红结点
if (parent.getRight().getRight()!=null &&
parent.getRight().getRight().getColor()==0 &&
parent.getRight().getLeft()!=null &&
parent.getRight().getLeft().getColor()==1){
parent.getRight().setColor(1);
parent.getRight().getLeft().setColor(0);
rightRound(parent.getRight());
parent.getRight().setColor(parent.getColor());
parent.setColor(0);
parent.getRight().getRight().setColor(0);
leftRound(parent);
}
//替换结点的兄弟结点的子结点都为黑结点
if (parent.getRight().getRight()!=null &&
parent.getRight().getLeft()!=null &&
parent.getRight().getRight().getColor()==0 &&
parent.getRight().getLeft().getColor()==0) {
parent.getRight().setColor(1);
evalTree(targetNode, parent);
return;
}
}
}
}
//替换节点是其父节点的右子节点
if (rNode.getChildType() == 1) {
if (parent.getLeft() != null) {
//替换节点的兄弟节点是红色
if (parent.getLeft().getColor()==1){
parent.getLeft().setColor(0);
parent.setColor(1);
rightRound(parent);
parent = rNode.getParent();
parent.getLeft().setColor(1);
evalTree(targetNode, parent);
return;
}
//替换结点的兄弟结点是黑结点
if (parent.getLeft().getColor()==0){
//替换结点的兄弟结点的左子结点是红结点,右子结点任意颜色
if (parent.getLeft().getLeft()!= null &&
parent.getLeft().getLeft().getColor() == 1) {
parent.getLeft().setColor(parent.getColor());
parent.setColor(0);
parent.getLeft().getLeft().setColor(0);
rightRound(parent);
}
//替换结点的兄弟结点的左子结点为黑结点,右子结点为红结点
if (parent.getLeft().getLeft()!=null &&
parent.getLeft().getLeft().getColor()==0) {
parent.getLeft().setColor(1);
parent.getLeft().getRight().setColor(0);
leftRound(parent.getLeft());
parent.getLeft().setColor(parent.getColor());
parent.setColor(0);
parent.getLeft().getLeft().setColor(0);
rightRound(parent);
}
//替换结点的兄弟结点的子结点都为黑结点
if (parent.getLeft().getLeft()!=null &&
parent.getLeft().getRight()!=null &&
parent.getLeft().getLeft().getColor()==0&&
parent.getLeft().getRight().getColor()==0) {
parent.getLeft().setColor(1);
evalTree(targetNode, parent);
return;
}
}
}
}
}
switchValue(targetNode, rNode);
removeNode(rNode);
}
/**
* 添加节点
* @param node
*/
public void addNode(Node node) {
//当前树为空,直接赋值退出
if (root == null) {
root = node;
root.setColor(0);
return;
}
node.setColor(1); //保证插入点是红色的
Node parent = searchInsertParent(node, root);
if (parent == null) {
return;
}
//插入节点的父节点是红色节点,此时一定存在pparent
if (parent.getColor() == 1) {
Node pparent = parent.getParent();
int childType = parent.getChildType();
//叔叔节点存在且为红色
if ((childType==0 &&
pparent.getRight()!=null &&
pparent.getRight().getColor()==1) ||
(childType==1 &&
pparent.getLeft()!=null &&
pparent.getLeft().getColor()==1)) {
parent.setColor(0);
if (childType == 0) {
pparent.getRight().setColor(0);
} else {
pparent.getLeft().setColor(0);
}
pparent.setColor(1);
if (pparent.getChildType() == 0) {
pparent.getParent().setLeft(null);
} else if (pparent.getChildType()==1) {
pparent.getParent().setRight(null);
}
if (pparent.getParent()!=null) {
pparent.setParent(null);
} else {
root=null;
}
//将祖父节点当做新节点插入
addNode(pparent);
return;
}
//叔叔结点不存在或为黑节点
if ((childType==0 && (pparent.getRight()==null||pparent.getRight().getColor()==0))||
(childType==1 && (pparent.getLeft()==null||pparent.getLeft().getColor()==0))) {
//插入结点的父亲结点是祖父结点的左子节点
if (parent.getChildType()==0){
//插入节点是父节点的左孩子
if (node.getChildType()==0){
parent.setColor(0);
pparent.setColor(1);
rightRound(pparent);
return;
}
//插入节点是父节点的右孩子
if (node.getChildType()==1){
leftRound(parent);
pparent.setRight(null);
parent.setParent(null);
addNode(parent);
return;
}
}
//插入结点的父亲结点是祖父结点的右子节点
if (parent.getChildType()==1) {
//插入节点是其父节点的右子节点
if (node.getChildType()==1){
parent.setColor(0);
pparent.setColor(1);
leftRound(pparent);
return;
}
//插入节点是其父节点的左子节点
if (node.getChildType() == 0){
rightRound(parent);
if (childType==0) {
pparent.setLeft(null);
} else if (childType==1){
pparent.setRight(null);
}
parent.setParent(null);
addNode(parent);
return;
}
}
}
}
}
/**
* 移除节点
* @param value
* @return
*/
public boolean removeNode(long value) {
//查找节点
Node targetNode = searchNode(value);
if (targetNode == null) {
return false;
}
removeNode(targetNode);
return true;
}
public void removeNode(Node targetNode) {
//删除的节点无子节点,直接删除
if (targetNode.getLeft()==null && targetNode.getRight()==null) {
if (targetNode.getParent() == null) {
root = null;
} else {
if (targetNode.getChildType() == 0) {
targetNode.getParent().setLeft(null);
} else if (targetNode.getChildType() == 1) {
targetNode.getParent().setRight(null);
}
targetNode.setParent(null);
}
return;
}
Node rNode=null;
if (targetNode.getLeft() != null && targetNode.getRight()==null) {
rNode = targetNode.getLeft();
} else if (targetNode.getLeft()==null && targetNode.getRight()!=null) {
rNode = targetNode.getRight();
} else {
rNode = findNextNode(targetNode.getRight());
}
evalTree(targetNode, rNode);
}
}
public static void main(String[] args) {
/**
* test for tree print
*/
// Node node = new Node(3);
// Node node1 = new Node(1);
// node1.setColor(1);
// Node node2 = new Node(5);
// node.setLeft(node1);
// node.setRight(node2);
// Node node3 = new Node(4);
// node3.setColor(1);
// Node node4 = new Node(0);
// Node node5 = new Node(2);
// node2.setLeft(node3);
// node1.setLeft(node4);
// node1.setRight(node5);
// RBTree rbTree = new RBTree(node);
//测试搜索
// Node result = rbTree.searchNode(5);
// if (result == null) {
// System.out.println("nil");
// }else {
// System.out.println(result.getValue());
// }
//测试打印
// rbTree.printTree();
//测试左旋
// rbTree.leftRound(node);
// rbTree.printTree();
//插入测试
RBTree rbTree = new RBTree(null);
rbTree.addNode(new Node(6));
rbTree.addNode(new Node(4));
rbTree.addNode(new Node(3));
rbTree.addNode(new Node(7));
rbTree.addNode(new Node(9));
rbTree.addNode(new Node(10));
rbTree.addNode(new Node(1));
rbTree.addNode(new Node(15));
rbTree.addNode(new Node(20));
rbTree.addNode(new Node(8));
rbTree.addNode(new Node(13));
rbTree.addNode(new Node(15));
// rbTree.addNode(new Node(14));
// rbTree.addNode(new Node(19));
// rbTree.addNode(new Node(17));
rbTree.printTree();
rbTree.removeNode(7);
rbTree.printTree();
//测试查询后继节点
// System.out.println(rbTree.findNextNode(rbTree.searchNode(9).getRight()).getValue());
}
7.哈希表
哈希表又称为散列表,根据散列函数f(key)和处理冲突的方法将一组关键字映象到一个有限的连续的地址集(区间)上,并以关键字在地址集中的“象” 作为记录在表中的存储位置,这种表便称为散列表,这一映象过程称为散列造表或散列,所得的存储位置称散列地址。
hash列表中散列函数除了计算散列值还需要能够处理处理哈希冲突(不同的key计算出了相同的散列值),解决hash冲突一般有一些几种方式:
1.开放寻址法:
一旦发生散列冲突就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址一定能找到。
开放寻址法:Hi=(H(key) + di) MOD m,i=1,2,…,k(k<=m-1),其中H(key)为散列函数,m为散列表长,di为增 量序列,可有下列三种取法:
1). di=1,2,3,…,m-1,称线性探测再散列;
2). di=1^2,(-1)^2,2^2,(-2)^2,(3)^2,…,±(k)^2,(k<=m/2)称二次探测再散列;
3). di=伪随机数序列,称伪随机探测再散列。
2.再次计算哈希值:
顾名思义就是发生冲突时再计算一次哈希值,通过不同的哈希算法来计算出新的哈希值,直到直到空的散列 地址为止。
3.链地址法(Java hashmap就是这么做的)
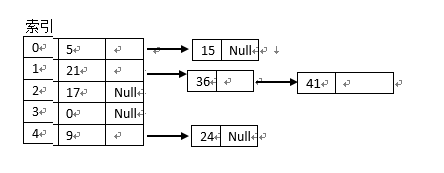
链地址法的基本思想是:每个哈希表节点都有一个next指针,多个哈希表节点可以用next指针构成一个单向链表,将所有关键字为同义词的结点链接在同一个单链表中,如:
设有 m = 5 , H(K) = K mod 5 ,关键字值序例 5 , 21 , 17 , 9 , 15 , 36 , 41 , 24 ,按外链地址法所建立的哈希表如下图所示:
4.建立一个公共溢出区
这种方法的基本思想是:将哈希表分为基本表和溢出表两部分,凡是和基本表发生冲突的元素,一律填入溢出表。
8.堆
堆是一种非线性结构,(本篇随笔主要分析堆的数组实现)可以把堆看作一个数组,也可以被看作一个完全二叉树,通俗来讲堆其实就是利用完全二叉树的结构来维护的一维数组
按照堆的特点可以把堆分为大顶堆和小顶堆
大顶堆:每个结点的值都大于或等于其左右孩子结点的值
小顶堆:每个结点的值都小于或等于其左右孩子结点的值
使用堆的目的是将最大(或者最小)的节点放在最前面,从而快速的进行相关插入、删除操作,所以在堆中进行搜索会很慢。堆不是用来加快搜索的,快搜索可以使用平衡二叉排序树或者红黑树。
10.图
常见的算法
冒泡排序
直接插入排序
简单选择排序
Java中常用的数据结构
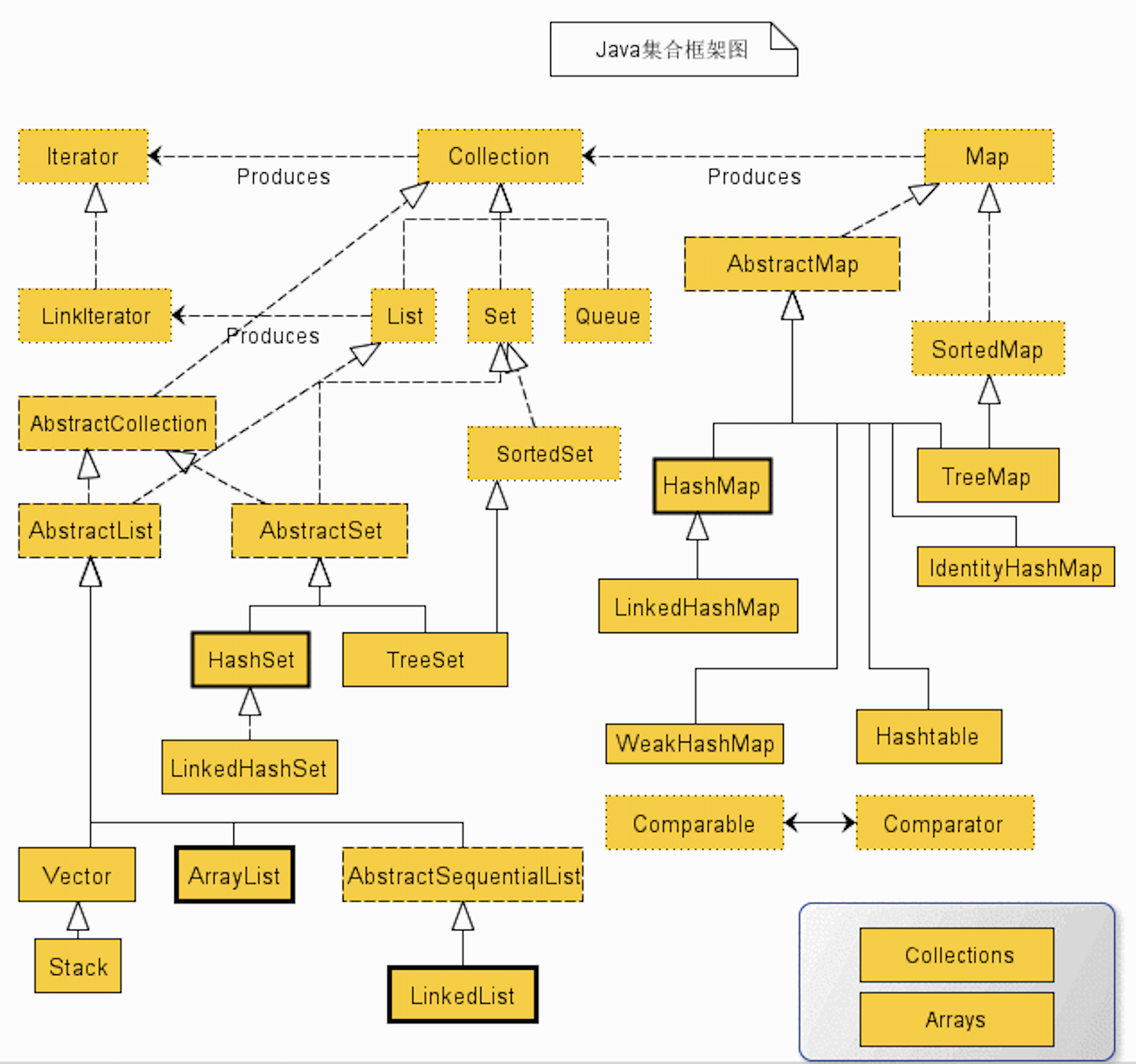
常用的List有:
ArrayList
ArrayList是基于数组实现的,访问元素效率快,删除插入元素效率低。
ArrayList内部维护了一个数组elementData,用于保存列表元素:
public E get(int index) {
if (index >= size)
throw new IndexOutOfBoundsException(outOfBoundsMsg(index));
return (E) elementData[index]; // 索引无需遍历,效率非常高!
}
public E set(int index, E element) {
if (index >= size)
throw new IndexOutOfBoundsException(outOfBoundsMsg(index));
E oldValue = (E) elementData[index];
elementData[index] = element; // 索引无需遍历,效率非常高!
return oldValue;
}
public void add(int index, E element) {
if (index > size || index < 0)
throw new IndexOutOfBoundsException(outOfBoundsMsg(index));
ensureCapacityInternal(size + 1); // 先判断是否需要扩容
System.arraycopy(elementData, index, elementData, index + 1, // 把index后面的元素都向后偏移一位
size - index);
elementData[index] = element;
size++;
}
public E remove(int index) {
if (index >= size)
throw new IndexOutOfBoundsException(outOfBoundsMsg(index));
modCount++;
E oldValue = (E) elementData[index];
int numMoved = size - index - 1;
if (numMoved > 0) {
// 把index后面的元素向前偏移一位,填补删除的元素
System.arraycopy(elementData, index + 1, elementData, index,
numMoved);
}
elementData[--size] = null; // clear to let GC do its work
return oldValue;
}
看下ArrayList的定义:
public class ArrayList<E> extends AbstractList<E>
implements List<E>, RandomAccess, Cloneable, java.io.Serializable
其中RandomAccess是快速随机访问的标识,ArrayList是数组实现的所以ArrayList可以实现快速随机访问元素。RandomAccess只是一个空的标识接口,这一点和Serializable相似。
/**
* ...
* <p>It is recognized that the distinction between random and sequential
* access is often fuzzy. For example, some <tt>List</tt> implementations
* provide asymptotically linear access times if they get huge, but constant
* access times in practice. Such a <tt>List</tt> implementation
* should generally implement this interface. As a rule of thumb, a
* <tt>List</tt> implementation should implement this interface if,
* for typical instances of the class, this loop:
* <pre>
* for (int i=0, n=list.size(); i < n; i++)
* list.get(i);
* </pre>
* runs faster than this loop:
* <pre>
* for (Iterator i=list.iterator(); i.hasNext(); )
* i.next();
* </pre>
* ...
*/
public interface RandomAccess {
}
支持快速随机访问的数据结构可以通过下标直接访问目标元素,这一点比使用迭代器访问效率高的多。在Collections中有很多基于快速随机访问的判断设计:
public static <T> int binarySearch(List<? extends Comparable<? super T>> list, T key) {
if (list instanceof RandomAccess || list.size()<BINARYSEARCH_THRESHOLD)
// 当List实现了RandomAccess或小于一定阀值时,使用索引二分查找算法
return Collections.indexedBinarySearch(list, key);
else
return Collections.iteratorBinarySearch(list, key);
}
ArrayList在创建时不指定容量大小,默认大小为10.ArrayList每次扩容至少为原来容量大小的1.5倍,在数组大小确定时使用ArrayList可以指定其容量大小来达到节约内存的目的。
Vector和Stack的细节
Vector和Stack我们几乎是不使用的了,所以并不打算用大篇幅来介绍,我们大概了解下就可以了。但我们可以探索下他们为何不受待见,从而引以为戒。
细节1:Vector也是基于数组实现,同样支持快速访问,并且线程安全
因为跟ArrayList一样,都是基于数组实现,所以ArrayList具有的优势和劣势Vector同样也有,只是Vector在每个方法都加了同步锁,所以它是线程安全的。但我们知道,同步会大大影响效率的,所以在不需要同步的情况下,Vector的效率就不如ArrayList了。所以我们在不需要同步的情况下,优先选择ArrayList;而在需要同步的情况下,也不是使用Vector,而是使用SynchronizedList(后面讲到)。你看,Vector处于一个很尴尬的地步。但我个人觉得,Vector被遗弃的最大原因不在于它线程同步影响效率——因为这毕竟能在多线程环境下使用——而在于它的扩容机制上。
细节2:Vector的扩容机制不完善
Vector默认容量也是10,跟ArrayList不同的是,Vector每次扩容的大小是可以指定的,如果不指定,每次扩容原来容量大小的2倍:
protected Object[] elementData; // 元素数组
protected int elementCount; // 元素数量
protected int capacityIncrement; // 扩容大小
public Vector(int initialCapacity, int capacityIncrement) {
super();
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal Capacity: "+
initialCapacity);
this.elementData = new Object[initialCapacity];
this.capacityIncrement = capacityIncrement;
}
public Vector(int initialCapacity) {
this(initialCapacity, 0); // 默认扩容大小为0,那么扩容时会增大两倍
}
public Vector() {
this(10); // 默认容量为10
}
public synchronized void ensureCapacity(int minCapacity) {
if (minCapacity > 0) {
modCount++;
ensureCapacityHelper(minCapacity);
}
}
private void ensureCapacityHelper(int minCapacity) {
// overflow-conscious code
if (minCapacity - elementData.length > 0) // 大于当前容量就扩容
grow(minCapacity);
}
private void grow(int minCapacity) {
// overflow-conscious code
int oldCapacity = elementData.length;
int newCapacity = oldCapacity + ((capacityIncrement > 0) ?
capacityIncrement : oldCapacity); // 默认扩容两倍
if (newCapacity - minCapacity < 0)
newCapacity = minCapacity;
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
elementData = Arrays.copyOf(elementData, newCapacity);
}
另外需要提醒注意的是,不像ArrayList,如果是用Vector的默认构造函数创建实例,那么第一次添加元素就需要扩容,但不会扩容到默认容量10,只会根据用户指定或两倍的大小扩容。所以使用Vector时指不指定扩容大小都很尴尬:
- 如果容量大小和扩容大小都不指定,开始可能会频繁地进行扩容
- 如果指定了容量大小不指定扩容大小,以2倍的大小扩容会浪费很多资源
- 如果指定了扩容大小,扩容大小就固定了,不管数组多大,都按这大小来扩容,那么这个扩容大小的取值总有不理想的时候
从Vector我们也可以反观ArrayList设计巧妙的地方,这也许是Vector存在的唯一价值了哈哈。
细节3:Stack继承于Vector,在其基础上扩展了栈的方法
Stack我们也不使用了,它只是添加多几个栈常用的方法(这个LinkedList也有,后面讨论),简单来看下它们的实现吧:
// 进栈
public E push(E item) {
addElement(item);
return item;
}
// 出栈
public synchronized E pop() {
E obj;
int len = size();
obj = peek();
removeElementAt(len - 1);
return obj;
}
public synchronized E peek() {
int len = size();
if (len == 0)
throw new EmptyStackException();
return elementAt(len - 1);
}
LinkedList的细节
细节1:LinkedList基于链表实现,插入删除元素效率快,访问元素效率慢
LinkedList内部维护一个双端链表,可以从头开始检索,也可以从尾开始检索。同样的,得益于链表这一数据结构,LinkedList在插入和删除元素效率非常快。
插入元素只需新建一个node,再把前后指针指向对应的前后元素即可:
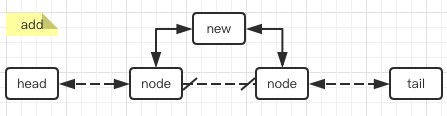
// 链尾追加
void linkLast(E e) {
final Node<E> l = last;
final Node<E> newNode = new Node<>(l, e, null);
last = newNode;
if (l == null)
first = newNode;
else
l.next = newNode;
size++;
modCount++;
}
// 指定节点前插入
void linkBefore(E e, Node<E> succ) {
// assert succ != null;
// 插入节点,succ为Index的节点,可以看到,是插入到index节点的前一个节点
final Node<E> pred = succ.prev;
final Node<E> newNode = new Node<>(pred, e, succ);
succ.prev = newNode;
if (pred == null)
first = newNode;
else
pred.next = newNode;
size++;
modCount++;
}
public void add(int index, E element) {
checkPositionIndex(index);
if (index == size)
linkLast(element);
else
linkBefore(element, node(index));
}
同样,删除元素只要把删除节点的链剪掉,再把前后节点连起来就搞定了:
E unlink(Node<E> x) {
// assert x != null;
final E element = x.item;
final Node<E> next = x.next;
final Node<E> prev = x.prev;
if (prev == null) {
// 链头
first = next;
} else {
prev.next = next;
x.prev = null;
}
if (next == null) {
// 链尾
last = prev;
} else {
next.prev = prev;
x.next = null;
}
x.item = null;
size--;
modCount++;
return element;
}
public E remove(int index) {
checkElementIndex(index);
return unlink(node(index));
}
但由于链表我们只知道头和尾,中间的元素要遍历获取的,所以导致了访问元素时,效率就不好了:
Node<E> node(int index) {
// 使用了二分法
if (index < (size >> 1)) { // 如果索引小于二分之一,从first开始遍历
Node<E> x = first;
for (int i = 0; i < index; i++)
x = x.next;
return x;
} else { // 如果索引大于二分之一,从last开始遍历
Node<E> x = last;
for (int i = size - 1; i > index; i--)
x = x.prev;
return x;
}
}
public E get(int index) {
checkElementIndex(index);
return node(index).item;
}
所以,LinkedList和ArrayList刚好是互补的,所以具体场景,应考虑哪种操作最频繁,从而选择不同的List来使用。
细节2:LinkedList可以当作队列和栈来使用
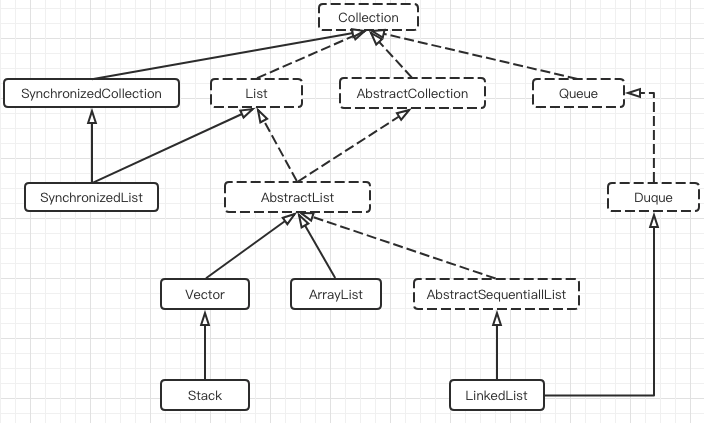
不知大家有没注意到在图2.2中,LinkedList非常“特立独行地”继承了Deque接口,而Deque又继承于Queue接口,这队列和栈的方法定义就是在这些接口中定义的,而LinkedList实现其方法,使自身具备了队列的栈的功能。
当作队列(先进先出)使用:
// 进队
public boolean offerFirst(E e) {
addFirst(e);
return true;
}
// 出队
public E pollLast() {
final Node<E> l = last;
return (l == null) ? null : unlinkLast(l);
}
当作栈(后进又出)来使用:
// 进栈
public void push(E e) {
addFirst(e);
}
// 出栈,如果为空列表,会抛出异常
public E pop() {
return removeFirst();
}
SynchronizedList的细节
在Collections类中提供了很多线程线程的集合类,其实他们实现很简单,只是在集合操作前,加一个锁而已。
细节1:SynchronizedList继承于SynchronizedCollection,使用装饰者模式,为原来的List加上锁,从而使List同步安全
先来看下SynchronizedCollection的定义:
static class SynchronizedCollection<E> implements Collection<E>, Serializable {
private static final long serialVersionUID = 3053995032091335093L;
final Collection<E> c; // 装饰的集合
final Object mutex; // 锁
SynchronizedCollection(Collection<E> c) {
this.c = Objects.requireNonNull(c);
mutex = this;
}
SynchronizedCollection(Collection<E> c, Object mutex) {
this.c = Objects.requireNonNull(c);
this.mutex = Objects.requireNonNull(mutex);
}
}
可以看到,可以指定一个对象作为锁,如果不指定,默认就锁了集合了。
再来看下我们关注的SynchronizedList:
static class SynchronizedList<E>
extends SynchronizedCollection<E>
implements List<E> {
final List<E> list;
SynchronizedList(List<E> list) {
super(list);
this.list = list;
}
SynchronizedList(List<E> list, Object mutex) {
super(list, mutex);
this.list = list;
}
...
public E get(int index) {
synchronized (mutex) {return list.get(index);}
}
public E set(int index, E element) {
synchronized (mutex) {return list.set(index, element);}
}
public void add(int index, E element) {
synchronized (mutex) {list.add(index, element);}
}
public E remove(int index) {
synchronized (mutex) {return list.remove(index);}
}
...
}
Java gc略解
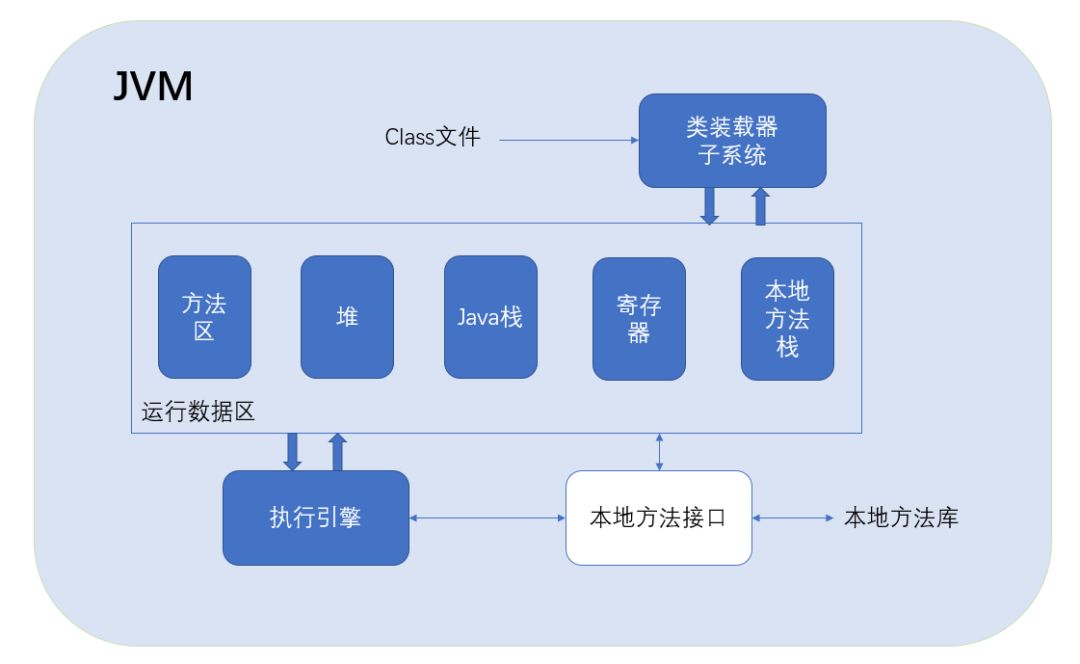
1、方法区
不止是存“方法”,而是存储整个 class文件的信息,JVM运行时,类加载器子系统将会提取 class文件里面的类信息,并将其存放在方法区中。例如类的名称、类的类型(枚举、类、接口)、字段、方法等等。
2、堆( Heap)
熟悉 c/c++编程的同学们应该相当熟悉 Heap了,而对于Java而言,每个应用都唯一对应一个JVM实例,而每一个JVM实例唯一对应一个堆。堆主要包括关键字 new的对象实例、 this指针,或者数组都放在堆中,并由应用所有的线程共享。堆由JVM的自动内存管理机制所管理,名为垃圾回收—— GC(garbage collection)。
3、栈( Stack)
操作系统内核为某个进程或者线程建立的存储区域,它保存着一个线程中的方法的调用状态,它具有先进后出的特性。在栈中的数据大小与生命周期严格来说都是确定的,例如在一个函数中声明的int变量便是存储在 stack中,它的大小是固定的,在函数退出后它的生命周期也从此结束。在栈中,每一个方法对应一个栈帧,JVM会对Java栈执行两种操作:压栈和出栈。这两种操作在执行时都是以栈帧为单位的。还有一些即时编译器编译后的代码等数据。
4、PC寄存器
pc寄存器用于存放一条指令的地址,每一个线程都有一个PC寄存器。
5、本地方法栈
用来调用其他语言的本地方法,例如 C/C++写的本地代码, 这些方法在本地方法栈中执行,而不会在Java栈中执行。
垃圾回收的基本过程:
1.Marking,将堆中的所有对象进行标记,标出其中的垃圾对象,
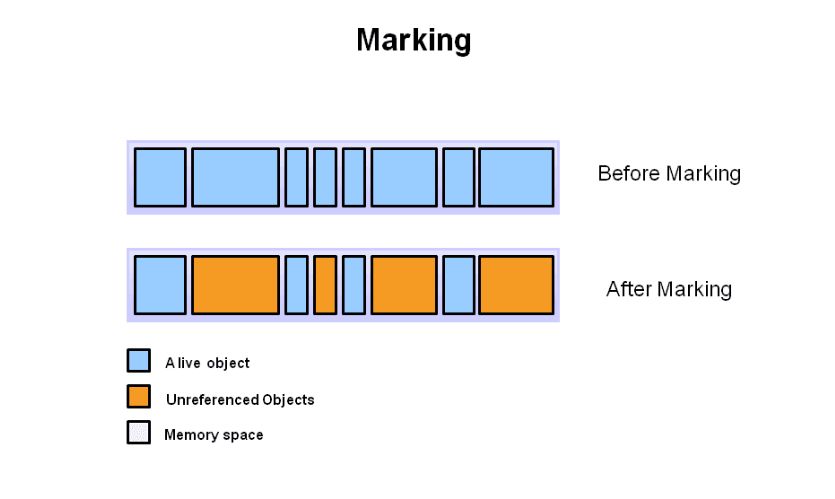
2.Normal Deletion,清除标记对象
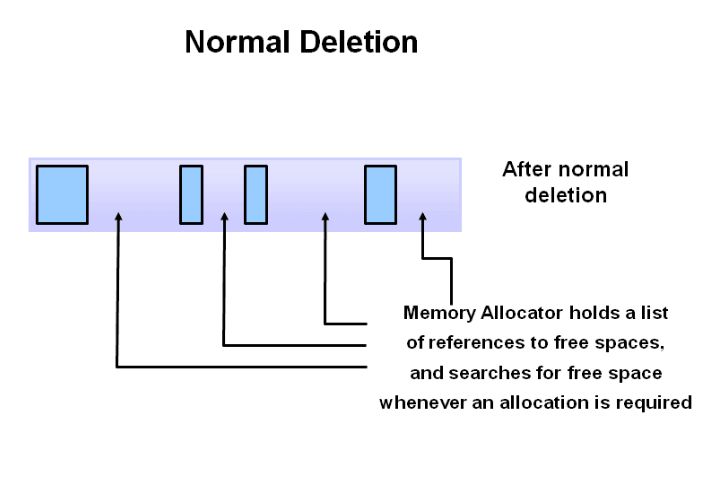
3.Deletion with Compacting,调整剩余对象的位置,压缩空间
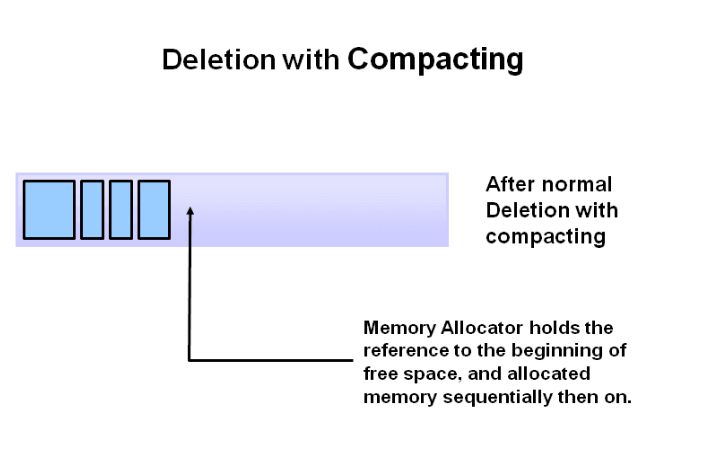
jvm垃圾收集的方法:
JVM并不是使用类似于 objective-c的 ARC(AutomaticReferenceCounting)的方式来引用计数对象,而是使用了叫根搜索算法( GC Root)的方法,基本思想就是选定一些对象作为 GC Roots,并组成根对象集合,然后从这些作为 GC Roots的对象作为起始点,搜索所走过的引用链( ReferenceChain)。如果目标对象到 GC Roots是连接着的,我们则称该目标对象是可达的,如果目标对象不可达,则说明目标对象是可以被回收的对象。
可以作为 GC Root的对象可以主要分为四种:
- JVM栈中引用的对象;
- 方法区中,静态属性引用的对象;
- 方法区中,常量引用的对象;
- 本地方法栈中,JNI(即Native方法)引用的对象;
通过以上的gc算法可以有效的标记出垃圾对象,当时随着对象的增多,垃圾收集的时间会不断增加。用于垃圾收集的时间大幅增加会降低程序运行的效率,难以满足我们的需求。所以,为了提高垃圾回收的效率,jvm对内存进行了分层,主要有:新生代,老年代和永久代。
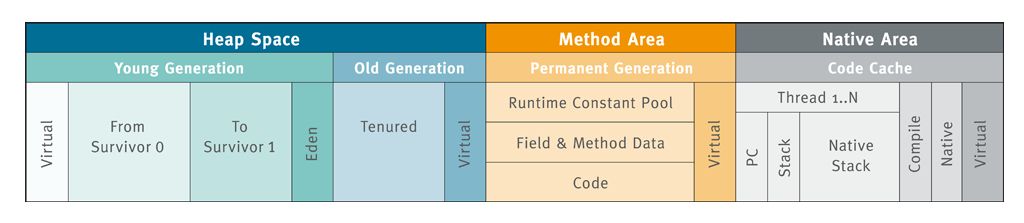
新生代
所有新产生的对象全部都在新生代中, Eden区保存最新的对象,有两个 SurvivorSpace—— S1和 S0,三个区域的比例大致为 8:1:1。当新生代的 Eden区满了,将触发一次 GC,我们把新生代中的 GC称为 minor garbage collections。 minor garbage collections是一种 Stopthe world事件,比如你妈在打扫时,会把你赶出去,而不是你一边扔垃圾她一边打扫。
我们来看下对象在堆中的分配过程,首先有新的对象进入时,默认放入新生代的 Eden区, S区都是默认为空的。下面对象的数字代表经历了多少次 GC,也就是对象的年龄。
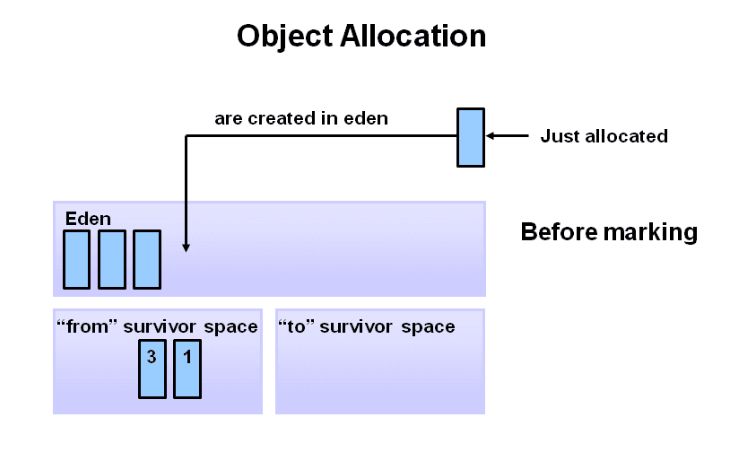
当 eden区满了,触发 minor garbage collections,这时还有被引用的对象,就会被分配到 S0区域,剩下没有被引用的对象就都会被清除。
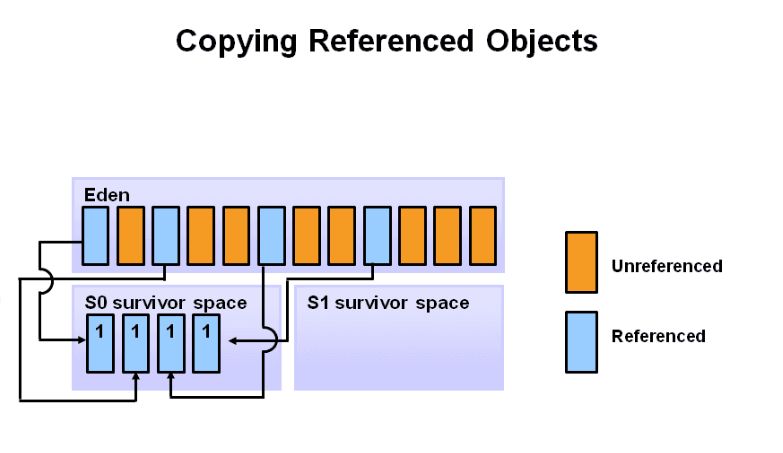
再一次 GC时, S0区的部分对象很可能会出现没有引用的,被引用的对象以及 S0中的存活对象,会被一起移动到 S1中。 eden和 S0中的未引用对象会被全部清除。
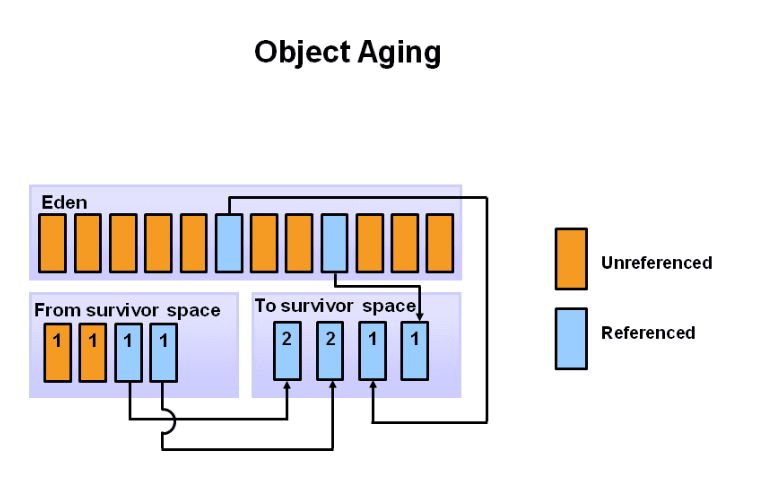
接下来就是无限循环上面的步骤了,当新生代中存活的对象超过了一定的【年龄】,会被分配至老年代的 Tenured区中。这个年龄可以通过参数 MaxTenuringThreshold设定,默认值为 15,图中的例子为 8次。
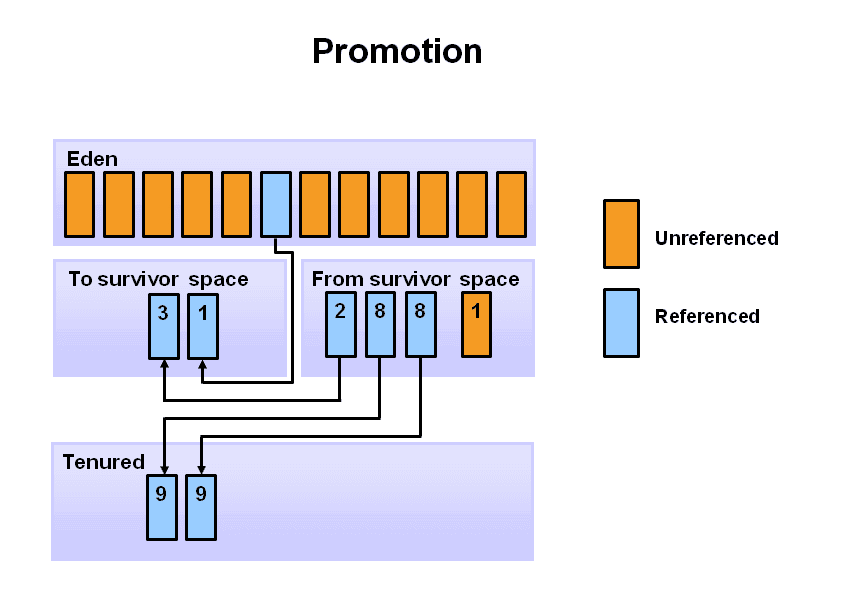
新生代管理内存采用的算法为 GC复制算法( CopyingGC),也叫标记-复制法,原理是把内存分为两个空间:一个 From空间,一个 To空间,对象一开始只在 From空间分配, To空间是空闲的。 GC时把存活的对象从 From空间复制粘贴到 To空间,之后把 To空间变成新的 From空间,原来的 From空间变成 To空间。
首先标记不可达对象
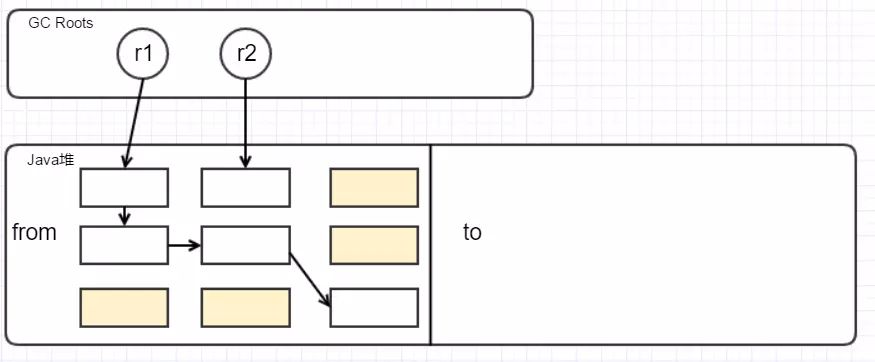
然后移动存活的对象到 to区,并保证他们在内存中连续
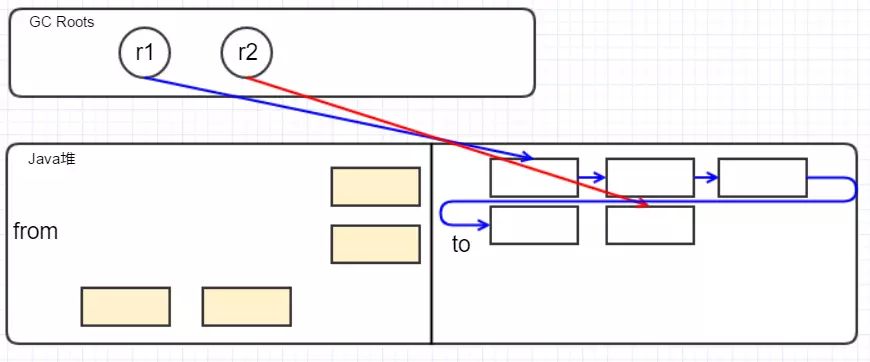
清扫垃圾
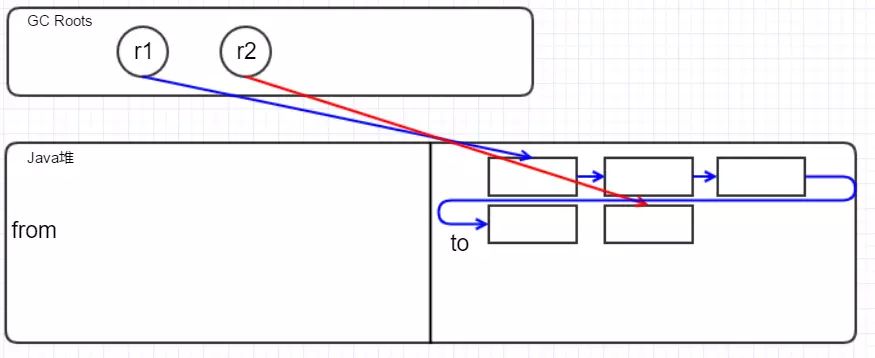
老年代
老年代用来存储活时间较长的对象,老年代区域的 GC是 major garbage collection,老年代中的内存不够时,就会触发一次。这也是一个 Stopthe world事件,但是看名字就知道,这个回收过程会相当慢,因为这包括了对新生代和老年代所有对象的回收,也叫 FullGC。
老年代管理内存最早采用的算法为标记-清理算法,这个算法很好理解,结合 GC Root的定义,我们会把所有不可达的对象全部标记进行清除。
在清除前,黄色的为不可达对象。
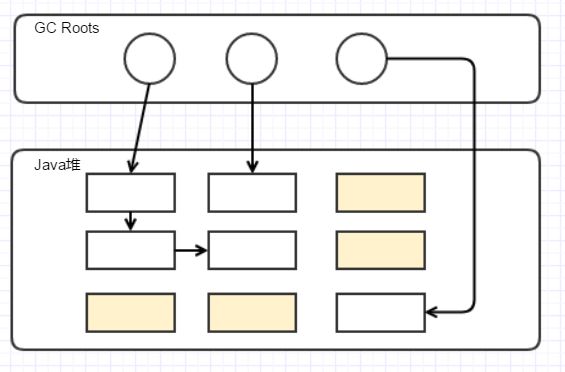
在清除后,全部都变成可达对象
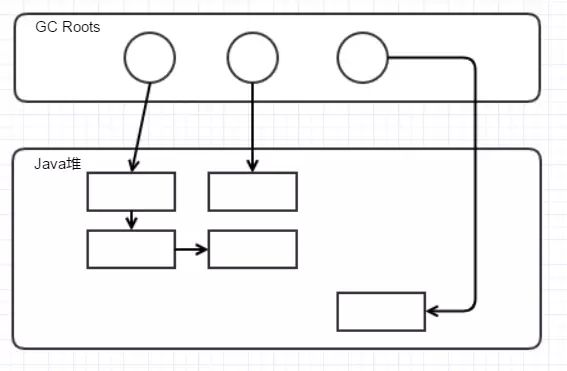
那么,这个算法的劣势很好理解:对,会在标记清除的过程中产生大量的内存碎片,Java在分配内存时通常是按连续内存分配,这样我们会浪费很多内存。所以,现在的 JVM GC在老年代都是使用标记-压缩清除方法,将上图在清除后的内存进行整理和压缩,以保证内存连续,虽然这个算法的效率是三种算法里最低的。
永久代
永久代位于方法区,主要存放元数据,例如 Class、 Method的元信息,与 GC要回收的对象其实关系并不是很大,我们可以几乎忽略其对 GC的影响。除了 JavaHotSpot这种较新的虚拟机技术,会回收无用的常量和的类,以免大量运用反射这类频繁自定义 ClassLoader的操作时方法区溢出。
gc优化
一般而言, GC不应该成为影响系统性能的瓶颈,我们在评估 GC收集器的优劣时一般考虑以下几点:
- 吞吐量
- GC开销
- 暂停时间
- GC频率
- 堆空间
- 对象生命周期
所以针对不同的 GC收集器,我们要对应我们的应用场景来进行选择和调优,回顾 GC的历史,主要有 4种 GC收集器: Serial、 Parallel、 CMS和 G1。
Serial
Serial收集器使用了标记-复制的算法,可以用 -XX:+UseSerialGC使用单线程的串行收集器。但是在 GC进行时,程序会进入长时间的暂停时间,一般不太建议使用。
Parallel
-XX:+UseParallelGC-XX:+UseParallelOldGCParallel也使用了标记-复制的算法,但是我们称之为吞吐量优先的收集器,因为 Parallel最主要的优势在于并行使用多线程去完成垃圾清理工作,这样可以充分利用多核的特性,大幅降低 gc时间。当你的程序场景吞吐量较大,例如消息队列这种应用,需要保证有效利用 CPU资源,可以忍受一定的停顿时间,可以优先考虑这种方式。
CMS ( ConcurrentMarkSweep)
-XX:+UseParNewGC-XX:+UseConcMarkSweepGCCMS使用了标记-清除的算法,当应用尤其重视服务器的响应速度(比如 Apiserver),希望系统停顿时间最短,以给用户带来较好的体验,那么可以选择 CMS。 CMS收集器在 MinorGC时会暂停所有的应用线程,并以多线程的方式进行垃圾回收。在 FullGC时不暂停应用线程,而是使用若干个后台线程定期的对老年代空间进行扫描,及时回收其中不再使用的对象。
G1( GarbageFirst)
-XX:+UseG1GC 在堆比较大的时候,如果 full gc频繁,会导致停顿,并且调用方阻塞、超时、甚至雪崩的情况出现,所以降低 full gc的发生频率和需要时间,非常有必要。 G1的诞生正是为了降低 FullGC的次数,而相较于 CMS, G1使用了标记-压缩清除算法,这可以大大降低较大内存( 4GB以上) GC时产生的内存碎片。
G1提供了两种 GC模式, YoungGC和 MixedGC,两种都是 StopTheWorld(STW)的。 YoungGC主要是对 Eden区进行 GC, MixGC不仅进行正常的新生代垃圾收集,同时也回收部分后台扫描线程标记的老年代分区。
另外有趣的一点, G1将新生代、老年代的物理空间划分取消了,而是将堆划分为若干个区域( region),每个大小都为 2的倍数且大小全部一致,最多有 2000个。除此之外, G1专门划分了一个 Humongous区,它用来专门存放超过一个 region 50%大小的巨型对象。在正常的处理过程中,对象从一个区域复制到另外一个区域,同时也完成了堆的压缩。
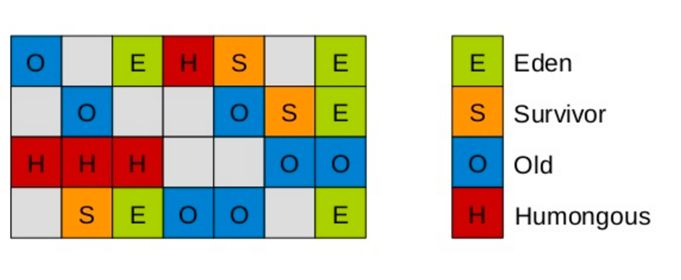
image
常用参数
-XX:+UseSerialGC:在新生代和老年代使用串行收集器
-XX:+UseParNewGC:在新生代使用并行收集器
-XX:+UseParallelGC :新生代使用并行回收收集器,更加关注吞吐量
-XX:+UseParallelOldGC:老年代使用并行回收收集器
-XX:ParallelGCThreads:设置用于垃圾回收的线程数
-XX:+UseConcMarkSweepGC:新生代使用并行收集器,老年代使用CMS+串行收集器
-XX:ParallelCMSThreads:设定CMS的线程数量
-XX:+UseG1GC:启G1垃圾回收器
Android的DVM和ART
什么是运行时?
简单来说,运行时就是一个供操作系统使用的系统,它负责将你用高级语言(比如 Java)编写的代码转换成 CPU/处理器能够理解的机器码。
运行时由你的程序运行时所执行的指令构成,尽管本质上它们不属于程序代码的任何一部分。
CPU (或者更通用的说法电脑)只能够理解机器语言(二进制代码),所以为了使程序能够在 CPU 上运行,就必须将它们翻译成机器码,这一工作由翻译器完成。
这里按序列出历代翻译器:
1.汇编器
它直接将汇编语言翻译成机器码,所以它的速度非常快。
2.编译器
它将源码翻译成汇编语言,然后再用汇编器转换成机器码。这种方式编译过程很慢但是执行速度很快。但是使用编译器最大的问题是编译出来的机器码依赖于特定的平台。换句话说,在一台机器上可以运行的代码在另一台不同的机器上可能就无法运行。
3.解释器
它在执行程序时才翻译代码。由于代码翻译是在执行阶段才发生,所以执行速度很慢。
JAVA 代码是怎么执行的?
为了使代码和平台无关,JAVA开发了 JVM,即 Java 虚拟机。它为每一个平台开发一个 JVM,也就意味着 JVM 是和平台相关的。Java 编译器将 .java 文件转换成 .class文件,也就是字节码。最终将字节码提供给 JVM,由 JVM 将它转换成机器码。
这比解释器要快但是比 C++ 编译要慢。
Android 代码是怎么执行的
在 Android 中,Java 类被转换成 DEX 字节码。DEX 字节码通过 ART 或者 Dalvik runtime 转换成机器码。这里 DEX 字节码和设备架构无关。
Dalvik 是一个基于 JIT(Just in time)编译的引擎。使用 Dalvik 存在一些缺点,所以从 Android 4.4(Kitkat)开始引入了 ART 作为运行时,从 Android 5.0(Lollipop)开始 ART 就全面取代了Dalvik。Android 7.0 向 ART 中添加了一个 just-in-time(JIT)编译器,这样就可以在应用运行时持续的提高其性能。
重点:Dalvik 使用 JIT(Just in time)编译而 ART 使用 AOT(Ahead of time)编译。
下图描述了 Dalvik 虚拟机和 Java 虚拟机之间的差别。
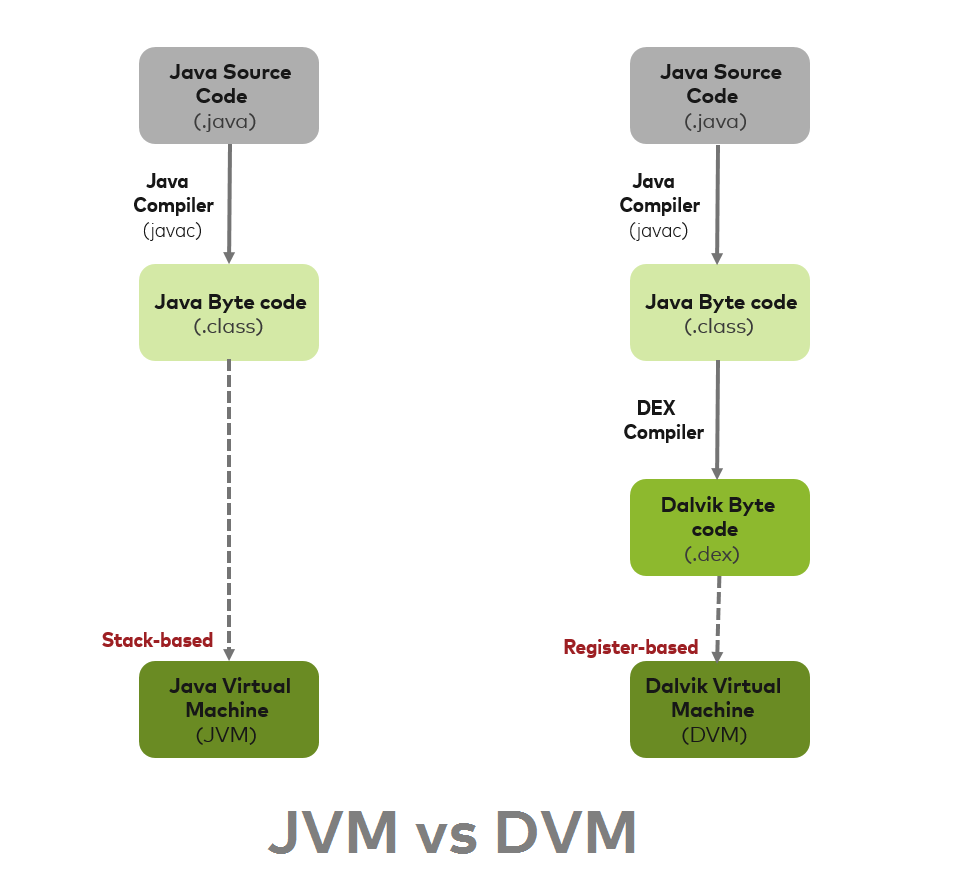
Just In Time (JIT)
使用 Dalvik JIT 编译器,每次应用在运行时,它实时的将一部分 Dalvik 字节码翻译成机器码。在程序的执行过程中,更多的代码被被编译并缓存。由于 JIT 只翻译一部分代码,它消耗的更少的内存,占用的更少的物理存储空间。
Ahead Of Time(AOT)
ART 内置了一个 Ahead-of-Time 编译器。在应用的安装期间,他就将 DEX 字节码翻译成机器码并存储在设备的存储器上。这个过程只在将应用安装到设备上时发生。由于不再需要 JIT 编译,代码的执行速度要快得多。
由于 ART 直接运行的是应用的机器码(native execution),它所占用的 CPU 资源要少于 使用 JIT 编译的 Dalvik。由于占用较少的 CPU 资源也就消耗更少的电池资源。
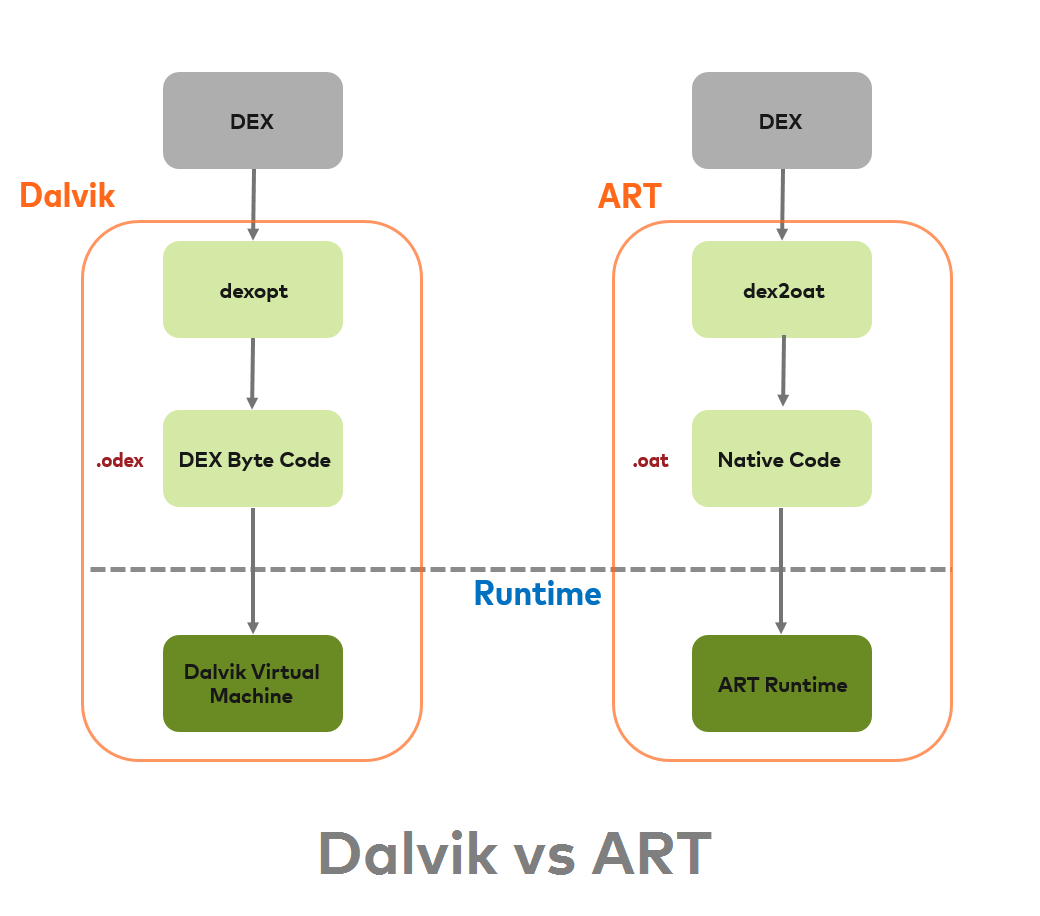
ART 和 Dalvik 一样使用的是相同的 DEX 字节码。编译好的应用如果使用 ART 在安装时需要额外的时间用于编译,同时还需要更多的空间用于存储编译后的代码。
Android 为什么要使用虚拟机?
Android 使用虚拟机作为其运行环境是为了运行 APK 文件构成的 Android 应用。它的优点有:
- 应用代码和核心的操作系统分离。所以即使任意一个程序中包含恶意的代码也不会直接影响系统文件。这使得 Android 操作系统更稳定可靠。
- 它提高了跨平台兼容性或者说平台独立性。这意味着即使某一个应用是在 PC 上编译的,它也可以通过虚拟机在移动平台上执行。
ART 的优点
- 应用运行更快,因为 DEX 字节码的翻译在应用安装是就已经完成。
- 减少应用的启动时间,因为直接执行的是 native 代码。
- 提高设备的续航能力,因为节约了用于一行一行解释字节码所需要的电池。
- 改善的垃圾回收器
- 改善的开发者工具
ART 的缺点
- 应用安装需要更长的时间,因为 DEX 字节码需要在安装时就翻译成机器码。
- 由于在安装时时生成的 native 机器码是存储在内部存储器上,所以需要更多的内部存储空间。
结论
DEX 是专门为 Android 设计的一种字节码格式,主要是为了消耗更少的内存进行优化。ART 是为了在低端设备上运行多个虚拟机而开发的,这一目的通过使用 DEX 字节码实现。它使得应用的 UI 反应更及时。这就是我个人的全部观点。更多关于 ART 和 Dalvik 的细节可以参考Android 官方文档。
Activity
1.activity在正常情况下的生命周期
2.activity在异常情况下的生命周期
3.activity的启动方式,隐式/显式
4.intent的匹配规则
Handler
消息循环的工作机制:Looper-Message
如何创建一个具有消息循环的线程:
class MyThread extends Thread{
@Override
public void run() {
super.run();
Looper.prepare();
Handler handler = new Handler() {
@Override
public void handleMessage(Message msg) {
super.handleMessage(msg);
//处理消息
}
};
Looper.loop();
}
}
小提示,Message.obtain()可以从缓存池中获得一个消息,Message使用完之后系统会调用recycle回收,建议不要使用new Message()。
handler产生内存泄露的几个点:
1.内部类产生的内存泄露:
final Handler handler = new Handler() {
@Override
public void handleMessage(Message msg) {
super.handleMessage(msg);
......
}
};
解决,使用静态内部类:
private static class MyHandler extends Handler{
//持有弱引用MainActivity,GC回收时会被回收掉.
private final WeakReference<MainActivity> mAct;
public MyHandler(MainActivity mainActivity){
mAct =new WeakReference<MainActivity>(mainActivity);
}
@Override
public void handleMessage(Message msg) {
MainActivity mainAct=mAct.get();
super.handleMessage(msg);
if(mainAct!=null){
//执行业务逻辑
}
}
}
2.Handler.post(Runnable)其实就是生成一个what为0的Message,调用:myHandler.removeMessages(0);会使runnable任务从消息队列中清除。
HandlerThread
一个现成的带有Looper消息循环的线程,
//内部Looper.prepare()
@Override
public void run() {
mTid = Process.myTid();
Looper.prepare();
synchronized (this) {
mLooper = Looper.myLooper();
notifyAll();
}
Process.setThreadPriority(mPriority);
onLooperPrepared();
Looper.loop();
mTid = -1;
}
使用示例:
public class MainActivity extends AppCompatActivity {
private HandlerThread thread;
static Handler mHandler;
@Override
protected void onCreate(Bundle savedInstanceState) {
super.onCreate(savedInstanceState);
setContentView(R.layout.activity_main);
//创建一个HandlerThread并启动它
thread = new HandlerThread("MyHandlerThread");
thread.start();
//使用HandlerThread的looper对象创建Handler
mHandler = new Handler(thread.getLooper(), new Handler.Callback() {
@Override
public boolean handleMessage(Message msg) {
//这个方法是运行在 handler-thread 线程中的,可以执行耗时操作,因此不能更新ui,要注意
if (msg.what == 0x1) {
try {
Thread.sleep(3000);
Log.e("测试: ", "执行了3s的耗时操作");
} catch (InterruptedException e) {
e.printStackTrace();
}
//这个方法是运行在 handler-thread 线程中的,可以执行耗时操作,因此不能更新ui,要注意
// ((Button) MainActivity.this.findViewById(R.id.button)).setText("hello");
}
return false;
}
});
//停止handlerthread接收事件
findViewById(R.id.button).setOnClickListener(new View.OnClickListener() {
@Override
public void onClick(View v) {
thread.quit();
}
});
//运行
mHandler.sendEmptyMessage(0x1);
}
}
需要注意的一点,HandlerThread如果不主动执行HandlerThread.quit()或者HandlerThread..quitSafely()方法这个线程会一直持续接受新的任务事件,所以在不需要使用线程的时候要记得退出回收线程。
AsyncTask
几个核心的方法:
onPreExecute
主线程中执行,异步任务执行之前,完成初始化等 操作。
doInBackground
线程池中执行,任务执行
onProgressUpdate
主线程中执行,用于更新进度条
onPostExecute
主线程中执行,异步任务执行之后,将异步任务的执行结果传递到主线程。
注意事项:
1)AsyncTask类必须在主线程加载 2)AsyncTask对象必须在主线程创建 3)execute方法必须在主线程调用 4)不要在程序中直接调用AsyncTask提供的4个核心方法 5)一个AsyncTask对象只能执行一次,即只能调用一次execute
源码分析,
AsyncTask调用过程一般是,定义一个异步任务继承自AsyncTask:
private class MyAsyncTask extends AsyncTask<String, Integer, String> {
protected String doInBackground(String... args1) {
Log.i(TAG, "doInBackground in:" + args1[0]);
int times = 10;
for (int i = 0; i < times; i++) {
publishProgress(i);//提交之后,会执行onProcessUpdate方法
}
Log.i(TAG, "doInBackground out");
return "over";
}
/**
* 在调用cancel方法后会执行到这里
*/
protected void onCancelled() {
Log.i(TAG, "onCancelled");
}
/**
* 在doInbackground之后执行
*/
protected void onPostExecute(String args3) {
Log.i(TAG, "onPostExecute:" + args3);
}
/**
* 在doInBackground之前执行
*/
@Override
protected void onPreExecute() {
Log.i(TAG, "onPreExecute");
}
/**
* @param args2
*/
@Override
protected void onProgressUpdate(Integer... args2) {
Log.i(TAG, "onProgressUpdate:" + args2[0]);
}
}
然后启动任务执行:
new MyAsyncTask().execute("AsyncTask Test");
核心就是execute的具体实现:
public final AsyncTask<Params, Progress, Result> execute(Params... params) {
return executeOnExecutor(sDefaultExecutor, params);
}
public final AsyncTask<Params, Progress, Result> executeOnExecutor(Executor exec,
Params... params) {
//判断当前状态
if (mStatus != Status.PENDING) {
switch (mStatus) {
case RUNNING:
throw new IllegalStateException("Cannot execute task:"
+ " the task is already running.");
case FINISHED:
throw new IllegalStateException("Cannot execute task:"
+ " the task has already been executed "
+ "(a task can be executed only once)");
}
}
//将状态置为运行态
mStatus = Status.RUNNING;
//主线程中最先调用onPreExecute方法,进行准备工作
onPreExecute();
//将参数传给mWorker
mWorker.mParams = params;
//调用线程池,执行任务
exec.execute(mFuture);
return this;
}
其中,sDefaultExecutor是一个单线程的串行线程池:
public static final Executor SERIAL_EXECUTOR = new SerialExecutor();
private static volatile Executor sDefaultExecutor = SERIAL_EXECUTOR;
private static class SerialExecutor implements Executor {
final ArrayDeque<Runnable> mTasks = new ArrayDeque<Runnable>();
Runnable mActive;
public synchronized void execute(final Runnable r) {
mTasks.offer(new Runnable() {
public void run() {
try {
r.run();
} finally {
scheduleNext();
}
}
});
if (mActive == null) {
scheduleNext();
}
}
protected synchronized void scheduleNext() {
if ((mActive = mTasks.poll()) != null) {
THREAD_POOL_EXECUTOR.execute(mActive);
}
}
}
所以直接执行execute方法,AsyncTask是串行执行的。通过调用excuteOnexcutor可以实现并行执行。
Binder
关于binder的所有内容:
在了解Binder是什么之前先明确一点,Binder有什么用?
Binder可以实现进程间通讯(IPC)。
那么,除了Binder之外还有哪些进程间通讯的方式呢?为什么我们需要通过Binder来实现进程间通讯而不使用其他的方式?
首先,进程间通信的方式我们一般常见的有:文件共享、AIDL、Messenger、ContentProvider和Socket等,这其中AIDL和Messenger以及ContentProvider底层又是通过Binder实现的。